Зачем писателю математика?
а ещё
Как выиграть спор?
если он об истории
Но иногда добросовестному историку приходится заниматься и математикой.
Нет для автора хуже, чем дать повод для спора - про оружие. Распространёнными являются в основном два метода достижения победы в «научном» споре:
- давить оппонента мнением авторитетов - и не замечать любые идущие в разрез факты
- если вышеописанный метод уже использует оппонент против вас - презирать любые авторитеты - и конечно же опять-таки не замечать факты
Оба метода хороши - если цель как следует разругаться. Но что делать, если хочется установить истину?
Действительно, было бы замечательно всегда отстаивать только истину. И просто обязательно знать истину, чтобы сочинить правдивый сюжет. Но в мире очень много авторитетов, все играют фактами и давно научились скрывать всё идущее вразрез. Как же узнать правду?
 | ||
 |
«Баллистический вычислитель» |  |
 |
Споры об оружии отличаются определённой спецификой. Некоторые становятся даже «извечными». Например, спор что лучше: лук или арбалет? Можно с упоением погрузиться в битву при Креси, при Азенкуре, вспомнить даже морское сражение при Слёйсе. Услышать про рекорды стрельбы - и про развенчание мифов. Но практически никогда ни один из спорщиков не коснётся самого главного - собственно оружия.
Достаточно воспользоваться его математической моделью - и как раз тут выручает «Баллистический вычислитель».
Пример № 1
Согласно древнегреческому инженеру Филону, самые большие, из состоявших на вооружении легионов, метательных машин, метали камни весом 26 кг на 200 м. Не многовато ли? Призванная сокрушать стены бастионов, осадная пушка стреляла 24-фунтовым ядром, то есть весом менее половины того камня, который бросала архаичная катапульта...
Если подлинную пушку мы может увидеть в музее, то вот подлинных катапульт до нашего времени не сохранилось. А кабы и сохранились, то пострелять из музейного экспоната никто не разрешит. Как же узнать, правдивы ли сведения Филона?
Только математика нас выручит. Вспоминаем школьные формулы, которым нас учили на уроках физики... что, забыли? Да я и сам их всё время забываю. Потому вот написал полезную программу и выложил на своём сайте SteamAge.ru в разделе «Программы» под названием «Баллистический вычислитель» - пользуйтесь на здоровье!
А я пока объясню, что нужно считать. Нас интересует мощь выстрела - её легко подсчитать по формуле кинетической энергии. Но мы знаем только вес ядра. Скорость этого ядра придётся угадывать. Исходить будем из условия: катапульта изготовлена к стрельбе на максимальную дальность. В школе нас учили, что таковая будет достигнута при угле бросания 45° (если пользуетесь моей программой, там в таблице «Выстрел» он уже по умолчанию так и выставлен). Попробуем пустить наш камень с вполне достижимой для торсионной метательной машины скоростью в 50 м/с. Снаряд улетел на 1/4 километра, что заметно дальше сведений Филона. Попробуем выпустить его со скоростью 40 м/с - теперь только 160 м, недолёт почти настолько же, каким был перелёт. Нужное значение скорости примерно посередине - задаём скорость 45 м/с, стреляем - результат 206 м. Правда мы пренебрегли сопротивлением воздуха, но для такой малой скорости и массивного снаряда ошибка будет не более пары процентов.
 | ||
 |
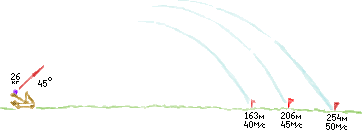 Схема к расчёту стрельбы катапульты для определения её мощности
Схема к расчёту стрельбы катапульты для определения её мощности
|  |
 |
Смотрим, какова же вышла мощь выстрела метательной машины - она более 26 кило-джоулей. Удобнее выразить это через килограммо-метры - развиваемое машиной усилие почти 2.7 тонны. Да, усилие немалое, но деревянные брусья его вполне могут выдержать. Вообще говоря, деревянные брусья уверенно выдерживают и куда большую нагрузку. А столь любимые греческими и римскими инженерами торсионы вполне могут развить такое усилие без каких-либо проблем - на каждый торсион здесь придётся примерно по 11/2 тонны. К примеру, такие ставят в подвеску современных джипов, и это далеко не предел для этих устройств. Даже древние торсионы могут легко развить мощь на порядок больше. И если сопоставить усилие менее 3 тонн с громадными каменными глыбами, уложенными в основание римских акведуков, то становится ясно что перед нами довольно заурядное техническое устройство античности. И мы вполне может принять как вывод, что подобные орудия могли строиться серийно и быть штатной артиллерией легионов.
Выходит античная катапульта не так уж сильно уступала пушке? Не совсем. По энергии выстрела этой рядовой катапульте соответствует вовсе не осадная, а заурядная 3-фунтовая полевая пушка. Её ядро, конечно, намного легче, зато летит дальше. Сама пушечка полегче, и на походе с ней меньше проблем. Наводить пушку на цель проще. Да ещё пушка картечью пальнуть может, чего катапульта не умеет. Правда катапульта не нуждается в порохе и от погоды не зависит (ведь в сильный ливень порох намокал, и стрелять становилось невозможно). Так что изредка катапульты могли находить себе применение, хотя скорее где-нибудь в колониях, а не в рядах регулярных армий.
Пример № 2
Профессор Эндрю Ламберт (Andrew Lambert), в интервью каналу «Discovery», высказал мнение, что лучшая метательная машина античности, в теории, могла выдать до 2.5 мега-джоулей, чего хватало чтобы метнуть снаряд весом 300 фунтов на 3 мили. Конечно, речь идёт об уникальной машине. Но девиз настоящего учёного «доверяй, но проверяй». Так мы и поступим.
Надо полагать речь о сухопутных милях. Английская сухопутная миля 1609 метров - что даёт 4827 м.
Теперь нужно определить вес снаряда. Для этого не обязательно лезть в справочники - идём на SteamAge.ru в раздел «Программы», где находим «Калибр и вес ядра». Выставляем фунты, вводим их число, нажимаем «расчёт» - а затем меняем единицы веса на килограммы. И сразу видим, что 300 английских фунтов это 136 кг. Теперь воспользуемся уже знакомым нам «Баллистическим вычислителем» - и видим, что энергия в 2.5 мДж может сообщить такому снаряду скорость почти в 192 м/с. Очень хорошая скорость, но смотрим ниже - как далеко улетит снаряд? Оказывается всего лишь примерно на 3750 м. Или 21/3 сухопутных мили. Увы, недолёт на 2/3 мили (больше километра).
Профессор ошибся?
Вероятнее всего профессор имел ввиду древне-римский фунт «либра», который изрядно легче английского фунта. Снова идём в «Калибр и вес ядра», и узнаём, что 300 «либра» это всего лишь чуть более 98 кг. При заявленной профессором энергии машины, она метнула бы такой снаряд со скоростью в 225 м/с. И, без учёта сопротивления воздуха, улететь он мог почти на 5.2 км. Скорость дозвуковая, поэтому для хорошо обтёсанного каменного ядра, чуть более 43 см диаметром, потери от трения о воздух будут относительно небольшие. Так что примерно 3 сухопутных мили пролететь оно могло. Уважаемый профессор оказался прав.
Другой вопрос, насколько часто встречались такие машины? Определённо это было громадное сооружение. С очень длинными рычагами, чтобы сообщать камню столь высокую скорость. И рычаги эти должны выдерживать при выстреле нагрузку не менее 255 тонн. Это большая нагрузка, и машина наверняка часто требовала ремонта. Когда для документального фильма по заказу BBC, построили реконструкцию подобной баллисты, она дала трещину уже после второго выстрела.
Возможно вникать в цифры Вам кажется скучным? Тогда программа «Осада замка» то что Вам надо. Можно легко и быстро нажатием кнопок менять и угол наведения и скорость снаряда - и тут же увидеть как именно полетит ядро, через сколько времени и где упадёт, и какова будет в этот момент его скорость. Теперь Вы знаете об этой полезной программе, и можно вернуться к нашим математическим упражнениям.
Пример № 3
А вот ещё одна извечная тема споров: лук против мушкета? Разумеется, скорость пули больше чем у стрелы, и расчёт выдаст в безвоздушном пространстве такую максимальную дальность для мушкета, которая лучникам и не снилась. Но не спешите с выводами. Обратите свой взгляд в последний раздел «Баллистического вычислителя», который называется «Дальность прямого выстрела».
Дело в том, что лучники стреляли, посылая свои стрелы навесом. Стрела летит не так быстро как пуля, в полёте стрелу видно - и по первой стреле можно корректировать следующие выстрелы. А вот мушкетёр свою пулю в полёте не видел. Мог только прицелиться поверх ствола. Потому стрелял мушкетёр исключительно прямым выстрелом.
Какой возьмём для сравнения лук? Если современный спортивный блочный (Compound bow), то он очень хорош. Стрелу он отправляет в полёт со скоростью почти в 90 м/с (около 100 ярд/с). Но это заслуга блоков, которые при идеальной конструкции в идеальных условиях могли бы дать прирост скорости вдвое. В реальности выходит меньше. Спортивный классический «обратно-изогнутый» лук (Recurve bow) пускает стрелу со скоростью около 67 м/с (почти 75 ярд/с). Этой скорости уже хватает, чтобы послать стрелу более чем на 400 м.
Но ведь это стало возможным только с современными материалами? В былые времена луки, разумеется, были хуже?..
И да, и нет. Действительно столь эффективных материалов, как нынче - не было. Но поинтересуйтесь, какова сила натяжения современных спортивных луков - она очень невысока, всего 20 кг или около того, что по средневековым меркам годится разве что для охоты. Боевые луки имели усилие натяжения около 50 кг. И этим компенсировалась недостаточная упругость тех луков.
При этом старинные азиатские композитные очень хороши, уж не уступят современным спортивным. Не случайно же турки, даже уже имея мушкеты, долго сохраняли лучников в армии. И боевой стрелой могли выстрелить вдвое дальше английского лучника, что наглядно продемонстрировал секретарь турецкого посольства в XVIII веке на собрании английского королевского клуба лучников. А специальную лёгкую стрелу посылали ещё дальше, рекорд более 700 м. Все эти сведения легко проверяются расчётом в «Баллистическом вычислителе». Дальность выстрела выходит даже больше реальной, но это потому, что мы не учитывали сопротивление воздуха. Однако такие рекордные луки требовали особо бережного обращения, особого хранения, и доступны были далеко не всем степным батырам. Впрочем, то как кочевники посылают свои стрелы едва ли не вдвое дальше - это неоднократно отмеченный современниками факт.
Но мы возьмём для сравнения самый рядовой простой английский длинный лук. Простой лук из единого куска дерева, будь он хоть из Индии, хоть из Африки, от английского (сделанного из испанского тиса) не сильно отличается. Рекорд дальности стрельбы из английского лука 225 м.
Про мушкеты можно встретить много самых разных сведений. Одновременно с лучниками на поле боя XV века встречались аркебузиры. Оценка возможностей их оружия такова: пуля в 20 г весом вылетала из ствола аркебузы со скоростью в 300 м/с.
 | ||
 |
 Вот почему мушкетёр не мог стрелять так же далеко как лучник
Вот почему мушкетёр не мог стрелять так же далеко как лучник
|  |
 |
И оказывается, что при стрельбе по ростовой мишени, стрела лука имеет шанс поразить таковую на дальности до 225 м - а вот пуля аркебузы туда даже не долетит!
Мы сейчас говорим только про дальность выстрела. Не в теории, а как на практике стреляли. А практически мушкетёру был доступен только прямой выстрел.
Выходит, заурядный лучник превосходил мушкетёра?
В какой-то период времени так и было. Но у порохового оружия было единственное, зато важное преимущество - простота обучения стрельбе из него. Это лучника нужно было учить с детства - не то он даже не смог бы боевой лук натянуть (для неподготовленного человека и 35 кг натяжение это ой-ёй-ёй). А в мушкетёры брали всякую деревенщину и через 40 дней получали дисциплинированных и исполнительных солдат.
Менялся и сам порох. Употреблявшаяся поначалу пороховая мякоть была крайне неудобной в использовании, а к тому же слабой. Через век придумали зернить порох - и такой стал гореть в 14 раз быстрее мякоти. Но его ещё били пестами. Не вручную, разумеется - большие песты приводили в движение мельницы, водяные либо ветряные. Но лишь к концу XVII века в Голландии изобрели расмалывание пороха жерновами - что делало его зёрна более однородными и плотными, горели они втрое сильнее прежнего зернёного пороха - это позволило заметно уменьшить количество пороха на каждый выстрел, а солдату добавило 3 лишних выстрела в боекоплект (было "12 апостолов" на неудобной перевязи - стало 15 патронов в патронташе на поясном ремне). И наконец Михайло Ломоносов создал оптимальный состав чёрного пороха. До него зачастую смешивали все компоненты в равных пропорциях - как в Европе, так и в Китае. Хотя, легендарный изобретатель пороха Бертольд Шварц имел свой секретный рецепт (впрочем, ни места проживания или работы, ни дат жизни Бертольда Шварца достоверно не известно). Известна тетрадь Роджера Бэкона, где он за век до знакомства европейцев с пороховым оружием (что произошло в Испании), описывает порох, впрочем с довольно неудачной рецептурой, в которой мало селитры. Так что рождение хорошего пороха произошло только перед самой Эпохой Пара. Кстати, к этмоу же моменту несколько улучшилось и качество изготовления мушкетов и единообразие отливки пуль для них.
И если взять для сравнения типичный стандартный армейский мушкет середины XIX века, то у него скорость пули 450 м/с. Теперь дальность прямого выстрела по ростовой мишени аж 270 м. Конечно куда интереснее поразить врага не в пятку (от этого только Ахилл умирал), а в туловище. Дальность выстрела по поясной мишени 200 м. Теперь мушкет уже вполне мог конкурировать с луком по дальности...
И опять точность
Если уж в Вашем произведении дойдёт до перестрелок лучников и мушкетёров, то хорошо бы знать, какова была техническая точность оружия. Об этом говорилось в прошлой главе. Но неплохо бы подкрепить слова историческими фактами.
Для лука тут всё плохо - или наоборот хорошо. У него точность целиком и полностью зависит от стрелка. И если ты не лучник - не бери в руки лук, только зря стрелы изведёшь. С другой стороны, уж если ты прирождённый лучник, то, после обучения, попадать будешь в меру своего таланта. На современных соревнованиях лучников, для стрельбы на самую дальнюю дистанцию в 90 м (100 ярдов) ставят мишень диаметром 122 см. Диаметр "10" на ней 122 мм, то есть менее человеческой головы. С другой стороны 122 см это по ширине 2.5 человека. И если мы наложим на мишень для лучников поясную фигуру - то наглядно увидим, что её (отдельно стоящего человека) поражают в среднем 1 стрела из 3 пущенных. И это в целом неплохо. Особенно если помнить, что в реальном бою стреляли не по отдельным человечкам, а по целым отрядам.
А вот мушкетёр, каким бы замечательным стрелком ни был, да только полностью зависел от своего мушкета. Так мог ли он попасть в цель на исчисленной нами дальности в 200 или даже 270 м?
История сохранила нам сведения лишь об одном эксперименте такого рода. Разыскал это в архивах и опубликовал уважаемый оружиевед и изобретатель Сергей Михайлович Кочкин (между прочим, автор более 70 запатентованных изобретений в сфере охотничьего оружия и боеприпасов). А нашёл он столь ценную информацию в книге дореволюционного оружиеведа и охотника Сергея Александровича Бутурлина. Вот результаты этого эксперимента:
| Дистанция в ярдах | Гладкоствольный мушкет 1842 | Карабин Миньё |
|---|---|---|
| число пробоин | ||
| 100 | 149 | 189 |
| 260 | 85 | 160 |
| 300 | 32 | 110 |
| 400 | 9 | 105 |
Бросается в глаза явная опечатка - 260 ярдов. Наверняка здесь должно быть 200 ярдов. Но именно в таком виде эта таблица напечатана в книге Кочкина, потому и я привожу её здесь в том же виде.
Тут, казалось бы, всё понятно: смотрим в последнюю строку и видим, что гладкостволки уступают штуцерам в дюжину раз. И многие вполне удовлетворятся этим. И даже иные оружиеведы. Вот только эти цифры не говорят ровным счётом ни о чём. А если присмотреться, то впору сильно озадачиться вопросом: а как вообще попали в мишень 9 пуль из гладкого ствола на дальности в 400 ярдов?
Начнём распутывать исторический ребус. Под названием мушкета 1842 года известен американский Спрингфилд модель 1842 капсюльный мушкет. Он одновременно является для американцев и первым и последним. Это последний гладкоствольный мушкет в армии США, но одновременно первый с капсюльным воспламенением и первый собираемый из взаимозаменяемых деталей, произведённых машинным способом. Заметим, что как у предшествующего ему мушкета 1840 года, ствол выпускался утолщённым в расчёте на возможность будущей нарезки. И позже действительно так и было сделано, полученная дульнозарядная винтовка стреляла пулей Миньё. Оба варианта - и гладкоствольный и нарезной - изрядно постреляли в Гражданскую войну между Севером и Югом. Ведь этих мушкетов было выпущено не менее 275 тысяч.
Вероятно, таблица и повествует нам об испытаниях двух модификаций этого мушкета - гладкоствольной и нарезной, полученной переделкой из гладкоствольной.
Однако мушкет этот не имел прицела с возможностью введения поправки на дальность. Поэтому неясно, как вообще прицеливались стрелки на дальностях свыше 200 ярдов? Максимум это 300 ярдов, что как раз равно 270 м для исчисленной нами стрельбы по ростовой мишени - да только на такой дальности пуля должна падать на землю у основания мишени. Видимо на 400 ярдов стрелки и вовсе брали «чуть-чуть повыше» - а сколько там получалось этого «повыше», то неведомо (может все пули дружно давали перелёт).
Неизвестно так же сколько именно было сделано выстрелов, но можно предположить, что выпускали 200 пуль на каждую дальность. Тогда всё замечательно, на 100 ярдов поражаем цель почти наверняка из любого оружия, на 200 ярдов - из гладкоствольного мушкета несколько менее половины выстрелов попадает в цель, а нарезной штуцер даёт результат вдвое лучше. Собственно далее 200 ярдов даже из штуцеров стрелять не полагалось. Да, были отдельные особо удачливые стрелки-снайперы, выстрелы которых расценивались современниками как настоящее чудо. Но если заглянуть в Уставы тех времён, то даже специально обученным прицельной стрельбе егерям команда открыть огонь подавалась не далее 200 шагов от врага. Хотя, как видим, штуцер середины XIX века замечательное оружие, каждый второй выстрел поражает цель и на 300 ярдов.
Да лучнику на эти 300 ярдов в жизнь стрелу не пустить... разве что он турок с турецким луком.
Но есть один нюанс ;-) Дело в том, что мишенью для испытаний мушкетов служила... площадка 25 на 25 шагов. Со стенкой высотой в человеческий рост. То есть мишень изображала целое подразделение - полное батальонное каре. Вот в этом и секрет такой замечательной меткости мушкетов и штуцеров - от них требовали всего лишь попадания в целый батальон. Тогда как лучники соревновались стрельбой по мишени изображавшей отдельно стоящего человека.
Пожалуй, на этом примере и закончим обсуждение, нужна ли писателю математика.
Легенда о Томасе Планкете
Начать придётся с того, что их было два. И оба застрелили вражеских генералов. Так что спутать одного с другим очень легко. Второй весьма удачным выстрелом убил генерала в Гражданскую войну Севера и Юга в США. Его фамилия оканчивается на «тт». Выстрел был удачным, но не чудесным. Легендой стал выстрел первого, случившийся более чем на полвека ранее. И его фамилия оканчивается на одно «т».
Как гласят просторы РУнета, в 1809 году, выстрелом из мушкета «Браун Бесс», рядовой солдат английской армии Томас Планкет убил французского генерала с 600 м. А затем, желая доказать своё искусство, вторым выстрелом убил адъютанта, бросившегося на выручку к своему генералу. Это, разумеется, самая категоричная версия. Более правдоподобные признают, что стрелял герой конечно же из штуцера. Но дистанция в 600 м повторяется везде как святая истина.
Однако англо-язычная Википедия не спешит подтвердить этот без сомнения выдающийся подвиг. Англо-язычная Вики вообще не уточняет дистанцию выстрела! Зато рассказывает больше других подробностей.
Томас Планкет был сержантом застрельщиков в Лёгкой бригаде. Лёгкая бригада это егеря, специально отобранные и обученные прицельной стрельбе. И даже не просто егеря - а егеря, обученные маскировке и подкрадыванию к врагу. У них даже форма была не яркая, а под цвет местности. Застрельщики это их самый передовой отрад - лучшие стрелки этой бригады обученных стрелков. И это не преувеличение. В битве при Ватерлоо в 1815 году, застрельщики этого же 95-го стрелкового полка в количестве взвода (около 28 стрелков), несколькими меткими залпами остановили наступление целого французского батальона, за несколько минут перебив всех офицеров противника.
Правда о меткости оружия этот факт нам ничего не сообщит. Палили более двух дюжин стволов, и, расстреляв почти весь боекомплект, убили пару офицеров. Это всё что известно. Ни дистанции стрельбы, ни сколько было поражено рядовых французских солдат - неизвестно. Ясно только, что, оставшись без командиров, и недоумевая, где же враг, французы решили не испытывать судьбу и повернули назад. Это не говорит о свойствах оружия застрельщиков лёгкой бригады - но говорит о их тактике и решимости.
А герой - их сержант, самый лучший стрелок среди лучших стрелков. И вооружён он был самым лучшим на тот момент времени оружием - штуцером Бейкера, который тогда выдавали лишь лучшим из лучших.
Дульнозарядный штуцер Бейкера образца 1800 года был первым в мире штуцером официально принятым на вооружение армии. До этого штуцеры уже использовались не первый век - но исключительно частным порядком. Например, во всех флотах мира считалось нормальным, чтобы капитан корабля за свой счёт вооружал штуцерами стрелков, из числа своих матросов. Что же побудило армию закупить штуцеры Бейкера за казённый счёт? Их замечательная точность.
Как утверждают англо-язычные источники, штуцер Бейкера уверенно поражал круглую мишень диаметром в рост человека с 200 ярдов. Запомните эту цифру!
Ибо, по Уставу, стрелять из штуцера далее 200 ярдов и не полагалось. И об этом, кстати, говорит и англо-язычная Википедия.
Как мы уже вычислили ранее - 200 ярдов это дальность прямого выстрела по грудной мишени. Дальность не равна точность! В XIX даже специально обученные прицельной стрельбе егеря не делали никаких поправок на дальность, не брали возвышение - им этого просто не полагалось Уставом, и на их оружии не имелось специальных прицелов для этого. Хотя в артиллерии таковые были. Но то артиллерия, ей и полагалось вдаль стрелять. А пехоте полагалось разбираться с целями поближе. Такое вот было разделение ратного труда - и его закреплял Устав.
Увидев приближающихся к мосту через речку французов, сержант Планкет сбросил свой ранец (так нередко делали, например, перед решительным броском в штыковую атаку), оставил цепь своих людей, и бросился вперёд. Пробежал 100 ярдов (хотя некоторые очевидцы оценивают дистанцию его выдвижения как 150 ярдов - другими словами настолько далеко вперёд, что его люди не смогли бы поддержать его огнём), и упал спиной на снег, удерживая штуцер и ногами - так считалось сподручнее стрелять из него. Дистанция выстрела - не указывается в Википедии.
Однако в Англии есть энтузиасты истории и реконструкторы. Они тщательно собрали все сохранившиеся свидетельства о выстреле Томаса Планкета, сверили их с местностью - и пришли к выводу, что сержант сблизился с целью примерно до 200 ярдов. Это всё равно остаётся очень удачным выстрелом. Ведь техническая точность этого оружия не гарантировала 100% попадания в человека на такой дистанции. И, возможно, дистанция была несколько больше 200 ярдов. Так что выстрел в любом случае - удачный. Но не чудесный. Вероятность попадания вполне нормальная, её можно оценить, как 1/3.
Непонятно почему адъютант не оказался рядом с генералом. Возможно, тот отослал его с приказом. Как бы то ни было, пока адъютант доскакал, сержант успел перезарядить своё оружие...
И это ещё одна небольшая загадка. Штуцер Байкера имел в боекомплекте два вида пуль - тяжёлую и лёгкую. Тяжёлая для дальней стрельбы на те самые 200 ярдов. Но её нужно было вколачивать в ствол (да, ударами деревянного молотка по шомполу) - так стреляли все штуцера в XVIII веке. Англичане этого не любили, и предпочитали немного схитрить - заряжать лёгкую пулю, завернутую в кусочек кожи. Введение этого хитрого приёма стрельбы - чисто ангийское изобретение, как раз введённое вместе с штуцером Байкера. Естественно, в этом случае заряжание очень быстрое (пуля в коже просто проталкивается в ствол шомполом за одно движение, стучать молотком не надо), обтюрация отличная (кожа не даст прорваться пороховым газам) - но вот про стабилизацию пули вращением можно забыть (из-за собственной инерции пуля будет проскальзывать в коже, должного числа вращений она не получит). Впрочем, на самом деле все штуцера той поры недокручивали пулю, причём недокручивали очень серьёзно. Так что проку от вращения было мало (если он вообще был хотя бы в минимальной степени) - зато, свойственная в то время именно штуцерам, хорошая обтюрация серьёзно улучшала результативность стрельбы. Но вылетая из ствола, лёгкая пуля тут же получала отклонение от его оси, из-за неравномерного обёртывания кусочком кожи. Возможно, сержант знал какой-то способ заворачивания пули в кожу более равномерно? Этого мы не узнаем.
Известно только, что когда адъютант подъехал, раздался второй выстрел из-за реки, оборвавший его жизнь. Вслед за тем, французская пехота остановилась в растерянности, а дюжина французских кавалеристов поскакала к мосту. Сержант успел добежать до линии своих стрелков раньше, чем разгневанные французы догнали его.
Вот собственно и вся история. Именно так она изложена в англо-язычных источниках. А откуда же тогда взялся миф о выстреле на 600 м?
Помните, я намекал: запомните эту цифру - 200 ярдов. В каждом ярде ровно 3 фута. Англичане нередко приводят расстояния в футах - а их тут получается 600... Да, это просто нелепая ошибка перевода, когда кто-то забыл пересчитать футы в метры, а остальные повторяли его слова, не проверяя источников.
Обычных линейных пехотинцев выстрелы бравого сержанта очень впечатлили. Линейной пехоте, вооружённой теми самыми мушкетами «Браун Бесс», Устав велел стрелять лишь с 55 ярдов и только залпом - в надежде, что хоть кто-то из всего строя попадёт. А тут человек стреляет на вчетверо большую дальность - и попадает два раза подряд не по батальону, а по отдельным людям!
Выстрелы Томаса Планета, заурядные по нынешним временам, тогда называли чудом. И это должно ясно указать нам на возможности оружия и солдат того времени. Нравится нам это или нет, но:
- никто не требовал, чтобы каждая пуля поражала цель - если попадал 1 выстрел из 3, это считалось отменной стрельбой. Именно такие требования были даже к лучшему штуцеру в мире на 1800 год
- мушкетёр уверенно стрелял на 50 ярдов - так велел ему Устав и это было не прихотью, а чётким пониманием свойств оружия и необразованного солдата
- специально обученный стрельбе егерь из штуцера уверенно стрелял на 100 ярдов (и 200 ярдов только если по вражескому батальону) - и так велел ему Устав (за нарушение которого в Англии могли и расстрелять)
- и лишь отлично подготовленный стрелок-инструктор сержант Томас Планкет позволял себе стрельбу на предельно вообразимые в те времена 200 ярдов, да к тому же по отдельным всадникам.
Ну а чтобы ни к кого не возникало соблазна сказать, мол, «это всё только математические выкладки», приведу вот эти слова, сказанные спустя почти 70 лет после тех чудесных выстрелов Томаса Планкета. Эпоха Пара уже подкатилась к самому своему концу, уже свершился переход на унитарный патрон с металлической гильзой и винтовку Бердана, а требования к точности оружия были - 1 попадание на 4 или 6 выстрелов по батальону. И сказано об этом не в частной беседе, а официально заявлено на заседании по вопросу о необходимости преобразований в стрелковом оружии по фактам Русско-Турецкой войны 1877-1878 годов:
 | ||
 |
О прицельной стрельбе винтовок XIX века«До 1870 года большей частью принимали, что деления на прицеле должны быть доведены до такой дистанции, с которой можно было бы разсчитывать попасть от 16% до 25% в сомкнутую часть.» Из доклада Н.П.Потоцкаго в Имперском Русском Техническом Обществе,
на беседе 21 января 1878 года, под председательством Н.Ф.Эгершторма |  |
 |
Это не всё!
А что если спор о битве при Креси? Генуэзские арбалетчики с намокшими тетивами стреляют по английским лучникам на вершине холма. Конечно, арбалет стрелял дальше простого лука. Но ведь тетива размокла. Но холмы-то там не такие уж высокие, вряд ли у лучников было преимущество высоты. Или всё же было? «Баллистический вычислитель» установить истину в этом случае не позволяет, ведь всё же цель и стрелок находятся на разном уровне. Да и желательно видеть траекторию выстрела.
 | ||
 |
«Осада замка» |  |
 |
Программа «Осада замка» вычисляет весь путь снаряда. И позволяет задавать высоту позиции и стрелка и цели, и расстояние между ними. От самого примитивного камнемёта до пушек Наполеона. А сверх того - точное время полёта снаряда до цели и его скорость в момент встречи с целью. Так же учитывается и влияние ветра.
И тогда можно наглядно увидеть, как воспетый в играх и фильмах якобы всесокрушающий требюше, не может сбить даже один зубец парапета дозорной башни - потому что скорость его каменного ядра слишком низка в этой точке траектории. Не менее Вы удивитесь, если зададите программе параметры полупудового шуваловского единорога, а затем, с помощью «Баллистического вычислителя», узнаете поражающую силу его ядра и сравните её с античной катапультой Филона. И немало ещё открытий готовы раскрыть перед Вами две эти программы.
P.S. Чуть не забыл. Старинные орудия обозначали не диаметром ствола, а весом ядра, да ещё нужно знать каменное было то ядро или чугунное, а может и свинцовое? Выручит программа «Калибр и вес ядра». Знаешь вес ядра - получишь диаметр ствола. Знаешь диаметр ствола пушки - узнаешь какого веса было ядро, а уж с этим можно за баллистические вычисления браться. А для любителей поразмышлять «а что было бы если...» программа «Калибр и вес ядра» позволяет узнать параметры даже для ядер из льда, серебра или урана.

 Публикации
Публикации Программы
Программы Игры
Игры Товары
Товары рГоблин
рГоблин