Кругла ли Земля?
в которой читатель узнаёт, что Земля была круглой всегда, но это не самая загадочная загадка картографии
 | ||
 |  | |
 |
Когда фантасты принимаются выдумывать миры с альтернативной историей, то часто пользуются «божественным произволом» (даже сам великий Профессор грешен в этом, ибо в середине повествования его «Сильмариллиона», мир из плоского становится шарообразным исключительно по прихоти Создателя). Но нельзя описывать а тем более объяснять нашу реальную историю с позиций такого же поверхностного взгляда!
Упрощая историю, мы упускаем многочисленные связи между народами - а они были! Как был и взаимообмен знаниями. Мы забываем о географических открытиях, которые в свою очередь оказались бы невозможны без решительных новшеств в военном деле и прежде всего в боге войны - артиллерии. И пусть даже порох не будет изобретён - не беда, появятся иные способы забрасывать снаряд на километры. Изобретения отдельных гениев и широкие перемены подготовлены и одновременно требует развития математики, картографии, навигации, баллистики. И все эти дисциплины зависят от вопроса: так кругла ли Земля?
История заблуждения
Прежде всего, заблуждением является, будто в нашей реальной истории древние верили в то, что Земля плоская. Если и верили, то точно не все. Достоверно известно, пифагорейцы утверждали что Земля шар. Ведь шар идеальная фигура. Но археологи находят искусственные шары, сделанные задолго до Пифагора (возраст иных уходит в Палеолит!), некоторые из них определённо изготовлены в ритуальных целях, и вполне возможно олицетворяли собой шарообразность Земли. Закреплённую, так сказать, религиозно.
Действительно, в буддистских текстах можно найти рассуждения о неких параллельных мирах - верхних и нижних. И даже их представление в виде пирамиды. Вот только это ни коим образом не означает, будто Будда завещал считать Землю плоской. В тибетской «Книге Мёртвых» ясно сказано, что все эти «миры» - суть один и тот же наш мир. Они параллельны в том смысле, что сосуществуют одновременно и вроде как каждый сам по себе - но в то же время пронизаны, по буддистским поверьям, сложной взаимосвязью взаимовлияний. Собственно, несмотря на своё устрашающее слух европейца название, «Книга Мёртвых» всего лишь текст, который монах должен растолковать умирающему, чтобы помочь тому преодолеть страх перед неизбежным и отойти в другой мир в умиротворённом состоянии. Но европейские переводчики, как обычно, перевели тексты в меру собственного невежества - вот откуда в европейской научной мысли возобладало заблуждение будто на Дальнем Востоке верили в плоскость Земли.
Сказки о Земле, покоящейся на слонах, которые стоят на черепахе - это именно сказки для маленьких детей. Судить по сказкам об уровне знаний древней цивилизации столь же глупо, как свести достижения космонавтики СССР к известным каждому советскому ребёнку стишкам Корнея Чуковского, где «крокодил солнце в небе проглотил». А сохраняются в памяти многих поколений не научные знания, а именно мифы и сказки по той же причине, по какой и ныне люди помнят всю жизнь услышанный в школе забавный хоть и бестолковый анекдот, но забывают наставления своего учителя математики чему равен синус 45°.
На деле же эта вера в будто плоскую Землю порождена исключительно христианством, да и то лишь в не слишком продолжительный период перед самой Эпохой Возрождения. Как раз тут начинает просыпаться широкий интерес к познанию мира - но увы, за средние века научные знания Европы крепко позабыты. Даже почитать нечего... кроме разве что святого писания.
И тут расцветает школа толкования библейских текстов. Нам от неё в наследство осталась система подкреплять свои научные труды ссылками - ведь именно ссылкой на соответствующий стих доказывали свою правоту средневековые богословы. И вот, выдёргивая отдельные фразы, и ни мало не заботясь о смысле, эти богословы в жарких спорах сошлись на том, что Земля де плоская и так де и записано по божьей указке.
Однако, справедливости ради, нужно упомянуть, что сама Церковь стремилась держаться в стороне от этих споров. К тому же многие из самоизбранных праведников-богословов были не слишком праведны с точки зрения официальной Церкви. Впрочем, иные из их противников были ни чуть не лучше (в частности Джордано Бруно, казнённый вовсе не за вращающуюся Землю, а за соучастие в своевременно пресечённом заговоре). Учёные же, которые в богословские игры (и сомнительные заговоры) не лезли, Церковь мало интересовали. Потому Коперник и Галилей на костёр не попали, а если из-за происков недоброжелателей их книги и запрещались, то чтоб вскоре быть снова разрешёнными.
Да иначе и быть не могло, ведь мореплавание перестало быть каботажным.
Когда скроются мачты
В основном мореплавание античности было каботажным - то есть вдоль берега, ввиду него. И желательно днём в хорошую погоду, чтоб видеть ориентиры на берегу. Эпоха Великих Географических Открытий это плавание Колумба на утлых судёнышках (один из его кораблей имел всего 22м в длину и 7½м в ширину, что примерно соответствует размерам не самого крупного торпедного катера). Бесшабашные смельчаки плыли по прямой - в открытый океан, у которого даже не знали есть ли конец (и не утянет ли их за край мира в вечный водопад)! А уж Средиземное море так и вовсе пересекали под любым углом.
Кабинетные богословы могли и дальше продолжать морочить головы деревенским простачкам, но моряки уже на практике видели, как исчезает корабль за горизонтом. Сперва скрывается его корпус, затем мачты, наконец вымпел на клотике - если бы море было плоским этого не происходило бы.
И тут вопрос круглая Земля или плоская переходил из теоретической плоскости в практическую. И не только ради открытия нового пути в Индию. Ведь на шаре кратчайшая линия пути отнюдь не прямая, а дуга. И на плоской карте она то же будет дугой (в некоторых случаях очень крутой - попробуйте прочертить кратчайший путь для перелёта из Баку в Вашингтон и он окажется дугой, выгнувшейся аж почти до Северного полюса). И вычислить верный курс можно только зная размеры земного шара. Не менее важны размеры земного шара для постройки маяков или приморских крепостей в новых колониальных владениях - как далеко будет видно свет маяка (или каков будет обзор с дозорной башни)?
Решить эту задачу помогает теорема Пифагора (ох, не зря он настаивал что Земля это шар).
 | ||
 |
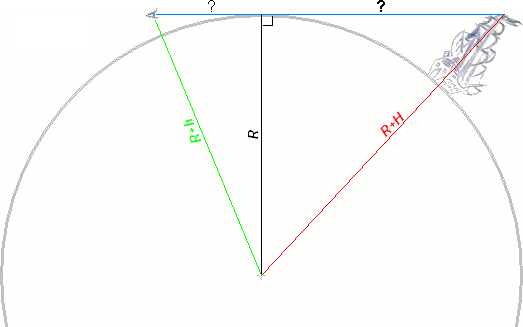 Как вычислить дальность видимости на планете используя теорему Пифагора
Как вычислить дальность видимости на планете используя теорему Пифагора
|  |
 |
Итак, по теореме мы знаем, что сумма квадратов катетов равна квадрату гипотенузы.
Так же мы знаем, что линия взгляда прямолинейна.
Для начала найдём, где у наблюдателя окажется край горизонта. Это наш первый знак вопроса. Очевидно, что видимый горизонт это точка где наша линия взгляда касается окружности Земли - а значит, она здесь проходит по касательной к этой окружности. В свою очередь касательная к окружности всегда перпендикулярна радиусу, проведённому из этой точки. Итак, мы обозначили пару катетов прямоугольного треугольника - один это радиус окружности Земли, а другой отрезок от глаз наблюдателя до пересечения линии взгляда с окружностью Земли - который нам и нужно найти.
А найти нам поможет гипотенуза. Гипотенузой у нас будет радиус Земли + высота до глаза наблюдателя.
К примеру, глаз рослого мужчины расположен на высоте 1.7м - и в результате вычислений получаем, что для него искомое расстояние до горизонта составит 4656м 79см.
Теперь второй знак вопроса - как далеко можно видеть флаг на корабельной мачте? Предположим, что высота мачты корабля 15м и проведём аналогичные вычисления для наблюдения из точки верхушки мачты - получим 13832м 73см до края горизонта.
А теперь сложим оба результата и получим 18489м 52см - то есть наблюдатель на берегу потеряет из виду верхушку мачты корабля, когда тот удалится почти на 18.5 км.
Как видим, даже древние могли решить подобную задачу... если б знали радиус планеты.
Как узнать радиус
Первым радиус Земли вычислил Эратосфен из Кирены (жил в 276 - 194 годах до н.э.), причём вычислил одновременно и довольно просто и достаточно точно. Что Земля это шар знали и до него, но размеры только предполагали, причём весьма ошибочно (так Архимед писал, что Земля имеет размер даже 3 миллиона стадиев, хотя и признавал что иные думают будто только 300 тысяч). Эратосфену это конечно было известно, недаром он с 30 лет глава Александрийской библиотеки (и оставался на этой должности 45 лет до самой своей смерти). А может быть, ему надоело прозвище «Бета», намекавшее, что он хоть и талантлив, но во всех науках только второй - вот он и решил хоть в чём-то стать первым. И вычислил радиус Земли.
 | ||
 |
Школьникам Эратосфен известен за своё «решето» - метод нахождения всех простых чисел. Метод достаточно остроумный, и жаль что в школе его лишь упоминают, но не объясняют. Суть его такова:
Оказывается чтобы найти все простые числа до числа N надо «просеять» их, делением на простые числа до |  |
 |
 | ||
 |
Александрийская библиотека пополнялась довольно интересным способом: каждый корабль, желавший торговать в Александрии, должен был привезти с собой какую-либо рукопись. Оригинал оставлялся в Александрии, но с него снималась копия, которая возвращалась владельцу корабля. Причём возвращалась в оригинальном переплёте - это было важно, так как богато украшенные переплёты обладали собственной значительной ценностью. Ценность же текстов для купцов была не столь очевидна. |  |
 |
Итак, Эратосфен жил в Александрии, но однажды узнал, что в Сиене...
(Сиена это современный Асуан... о, на память сразу приходит одна из величайших строительных афёр XX века, Асуанская плотина, которую провернули французы, ухитрившись продать песок из Индии - в Сахару! Причём речной! а с ним бетон получается в несколько раз хуже. А значит бетона для строительства потребуется намного больше. Так они ещё и бетон свой втюхали египтянам! простите, отвлёкся)
...которая расположена к югу от Александрии, в день летнего солнцестояния, освещается дно даже самых глубоких колодцев, что подтверждают и жители города и бывавшие там путешественники. Это могло означать лишь одно - Солнце в этот день над Сиеной в зените. То есть строго над головой. Эратосфен полагал что Солнце очень далеко от Земли, а значит его лучи можно считать практически параллельными. Следовательно, остаётся лишь в этот же день замерить угол падения лучей в Александрии, из этого угла получить угол дуги, ну а зная его и расстояние между городами, остаётся только перемножить чтоб получить длину окружности Земли.
 | ||
 |
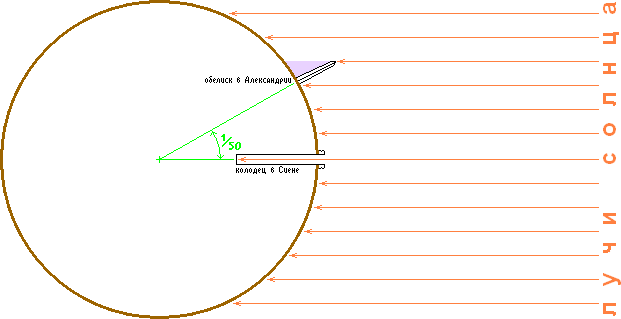 Как Эратосфен вычислил окружность Земли
Как Эратосфен вычислил окружность Земли
|  |
 |
Как же найти угол?
Эратосфен использовал гномон - примитивный по сути инструмент, вертикальный столб на ровной горизонтальной площадке, у которого замеряют длину тени (точнее в качестве такого гномона Эратосфен использовал большой обелиск, высота которого была ему известна). Несмотря на свою примитивность, гномон инструмент полезный. Самая короткая его тень ровно в астрономический полдень - и она же точно указывает на север (точнее, чем магнитный компас). Именно в полдень, в день летнего солнцестояния, Эратосфен и измерил длину тени в Александрии - в это же время в Сиене длина тени была равна нулю. А вот в Александрии, по подсчётам Эратосфена вышло, что угол составил 1/50 окружности.
Расстояние же между городами, Эратосфен узнал от погонщиков караванов, которые сказали, что верблюд проходит в день примерно 100 стадиев, а путь от Александрии до Сиены 50 дней. Итого 5 тысяч стадиев. 1/50 окружности соответствует 5000 стадиев, то вся окружность 250 тысяч стадиев. Но видимо Эратосфен позже провёл более точные измерения или узнал более точное расстояние из книг Александрийской библиотеки, так как в итоге указал длину окружности в 252 тысячи стадиев. Если он опирался на египетский стадий, равный 157.5м, то его результат 39690км, что не так уж сильно отличается от современной сферической модели Земли, в которой её радиус принят 40030.2км
Лучшее враг хорошего
Может показаться, что если взять дугу побольше, то погрешность станет меньше. Примерно по этому пути пошёл в своих вычислениях философ-стоик Посидоний (жил около 130 - 50 г до н.э.). Из своей обсерватории на Родосе он наблюдал звезду Канопус (вторую по яркости на небосводе) в точности над горизонтом, а при наблюдении из Александрии угловая высота этой звезды равна 1/48 земной окружности.
1/48 больше 1/50, а значит результат вычисления будет точнее, чем у Эратосфена.
Согласно Клеомеду, Посидоний считал что длина дуги меридиана между Родосом и Александрией 5000 стадиев, таким образом вся окружность вышла в 240 тысяч стадиев. Но Страбон (жил в 63 - 24г до н.э.) указывает, что позже расстояние между Родосом и Александрией было уточнено и составило только 3750 стадиев - отчего вся Земля «ужалась» до всего лишь 180 тысяч стадиев. Или по-современному 28350км.
Ошибка Посидония была в преломлении лучей атмосферой Земли, чего древний грек не знал. Потому хотя метод и геометрически верен, но выбор светила вблизи горизонта привёл к оптическому обману. Однако потомки не подвергали сомнению исчислений Посидония и в XV веке. Потому и Колумб считал Землю на ¼ меньше её истинного размера и до самой своей смерти был уверен, что открыл новый путь в Азию. Если бы он знал, что на пути встретится Америка, то наверное и плыть раздумал бы - ведь плыл он за азиатскими специями, которые ценились в то время едва ли не дороже золота.
Писателям-фантастам полезно не забывать о свойствах атмосферы выдуманного мира - ведь свойства эти, как видим, могут весьма значительно поменять мировоззрение аборигенов. Самый яркий такой пример это произведение братьев Стругацких «Обитаемый остров», где рассматривается планета с атмосферой, настолько сильно искривляющей лучи у горизонта, что удаляющийся корабль кажется поднимающимся вверх, отчего жители уверены будто живут внутри шара.
Триангуляция
Измерить длину на местности бывает сложно, а вот измерить угол довольно легко. И измерять углы на местности умели ещё древние римляне, и они вовсе не были в этом первыми. Собственно римским изобретением является только второй деревянный гвоздь на пилуме (коротком метательном копье особой конструкции), введённый лично консулом Марием, а всё остальное заимствовано у соседей, включая и тот самый пилум.
Но римляне ещё глобальной триангуляцией не озадачивались - их вполне устраивало каботажное плавание и путешествие по благоустроенным дорогам, которые на удивление прочнее любого современного шоссе даже сейчас, прослужив более 2 тысяч лет, без единого ремонта (и кто-то ещё говорит о прогрессе? может тогда и не было iPad, зато уж дороги строить умели). А вот после XV века потребность в точных картах становилась всё более насущной с каждым годом. И когда проблема вышла на государственный уровень, то и решить её в масштабах всего государства оказалось возможным.
Собственно триангуляция это построение треугольника на местности. Выбирают пару точек - как правило хорошо заметных ориентиров - между которыми расстояние достоверно известно. От них, визированием, находят угол на третью удалённую точку. Ну а, зная базу и углы, легко вычислить и расстояние. Затем можно строить новый треугольник, опираясь на вычисленные расстояния как на новую базу.
Вот так провели триангуляцию всего французского побережья в 1682 году. Заодно вычислили новую длину земного меридиана (которая пригодилась Ньютону для подтверждения его закона всемирного тяготения). Но самое забавное событие произошло, когда новую уточнённую карту побережья показали Людовику XIV. А дело в том, что выяснилась неточность прежних карт и новая уточнённая линия побережья значительно сместилась в сторону суши. Увидев это, король-солнце упрекнул учёных: "Ваше путешествие стоило мне части моего королевства!"
Откуда взялись градусы
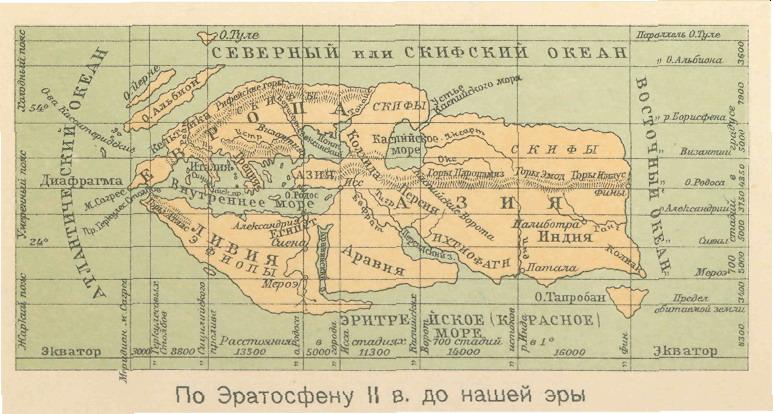
Карту с сеткой меридианов и параллелей (правда неправильной) составлял ещё Эратосфен. Но упорядочил эту сетку, сделав интервалы равными, только Гиппарх Никейский (жил около 180 - около 120г до н.э.). В его карте обитаемого мира было 11 параллелей. Он так же предлагал определять широту, одновременно наблюдая лунные затмения. Но главное, он первым из древних греков использовал известную нам градусную меру, в которой окружность делится на 360°
 | ||
 |
|  |
 |
Однако не Гиппарх это изобрёл. Он всего лишь воспользовался системой вавилонян. И по их же образцу делил далее каждый градус на 60 минут (записывается 60'), а вслед за тем каждую минуту на 60 секунд (60").
А теперь учтём, что для земной окружности, угловая мера в 1" соответствует расстоянию на окружности примерно в 31м...
Вопрос не в том, возможно ли было в древности измерить угол с такой точностью. Конечно возможно. Человеческий глаз на удивление точный инструмент, если создать ему соответствующие условия для работы. И речь не идёт о таких выдающихся представителях человеческого рода, как к примеру жители степей, которые с 5км замечают человека, высунувшего голову из-за валуна, а с 18км различают всадника на коне. Даже совсем не выдающийся обычный европейский горожанин способен различить на просвет щель в 2 микрона.
Вопрос в том - зачем? Вот римляне могли измерять углы - а триангуляцию империи не проводили. Хотя империя от Константинополя до Британии размахнулась на весь нынешний Евросоюз, не говоря об африканских владениях. И по всей её территории строили дороги (которыми европейцы пользовались до самого XX века, а в самой Италии пользуются и сейчас). Дороги это ещё пустяк в сравнении с акведуками, подводившими воду за десятки, а то и сотни километров. Вот уж где точно требовался точный план местности, выверенные углы и особенно уклоны. Высшее мастерство показали римские водопроводчики в ближне-восточных владениях римлян, где для иных новых колоний порой пришлось вести водопроводы в полторы сотни километров, то перебрасывая акведуки через бездонные ущелья, то прорубая в скалах тоннели. Ещё раз напомню, римский водопровод не заключён в трубу, это просто открытый жёлоб с равномерным уклоном, по которому вода течёт самотёком из горного источника до города. И уклон должен строго выдерживаться на всём протяжении такого водопровода, иначе где-то вода будет хлестать через край, а где-то застаиваться. И ведь выдерживали - по обнаруженным следам при проходке такого тоннеля двумя бригадами с двух сторон, расхождение в точке встречи (которое определено по следам зарубок от кирок на стенах тоннеля - не будем забывать никаких бурильных лазеров у римлян не было, всё строили руками) вышло всего в полметра, что неплохой результат и поныне даже для куда более скромных строек. Римский водопровод куда большее чудо света чем египетские пирамиды. Куда большее как по масштабам сооружений в целом, так и по размерам использованных камней (между делом поинтересуйтесь гранитными «кирпичиками» в основании некоторых сохранившихся до наших дней акведуков в Южной Франции).
(меня одного удивляет, отчего все учёные спорят о внеземном происхождении пирамидальных горок камней, но никто в упор не видит как в несколько раз большие камни - причём действительно камни - лежат посреди Европы в сложных арочных сооружениях)
Однако проблема в том, что систему угловых мер римляне через греков унаследовали от вавилонян... которые жили меж двух рек, воды в избытке, водопроводы не строили, строительством вечных шоссе не озаботились. Ну а для своих чудесных сооружений как Вавилонская Башня (то же почему-то причисленная к Чудесам Света) и толстенные крепостные стены, использовали необожжённый кирпич. Да и то, как показали раскопки, из кирпича складывали лишь тонкие внешние стенки, а толщу меж ними засыпали грунтом. Дёшево и сердито. И сколь-нибудь точные измерения углов для такой архитектуры не требуются. Кстати и сама воспетая башня была набором кубов, поставленных один на другой, а уж прямой угол тысячи лет назад размечать умели, с помощью верёвки с соотношением сторон 3:4:5 (да-да, именно отсюда, у вавилонян, позаимствовал Пифагор образец, на котором доказал свою теорему о «штанах»)
Итак, мы стоим перед фактом: вавилоняне не нуждались в градусной системе вообще. Во всех практических задачах их вполне удовлетворял прямой угол и каким-то образом они уже знали что треугольник со сторонами 3:4:5 является прямоугольным (и пользовались этим - но вот доказать не умели и это пришлось делать позже Пифагору). Тем не менее, именно они дали миру градусную систему мер, да вдобавок ещё точную настолько, что мельчайшая её мера 1 угловая секунда соответствует в масштабах земного шара расстоянию в 31м.
Даже римляне в период расцвета своей империи не нуждались в измерении всей планеты, к тому же с такой точностью.
Тем более, зачем это было вавилонянам, жившим в узком пространстве меж Тигром и Евфратом?
Напрашивается лишь одно логичное объяснение: вавилоняне не изобретали ни теорему Пифагора, ни градусную меру, а унаследовали какие-то обрывки знаний от предыдущей цивилизации. Очевидно более развитой. И не просто владевшей математикой и геометрией как минимум в пределах геометрии Евклида, но имевшей потребность в точных измерениях. Я бы даже сказал - массовую потребность в весьма точных и масштабных измерениях. Вроде геопозиционирования. Ведь погрешность в 1" при определении положения на земном шаре это типичная погрешность современного дешёвого GPS-навигатора...
Расплющил Землю
До XVII века Земля считалась идеальным шаром. Но затем один английский алхимик, всю жизнь положивший на поиски философского камня, между делом сидел под яблоней. Звали этого алхимика Исаак Ньютон (жил в 1643 - 1727г). Следствием грохнувшегося ему на голову яблока, стал закон всемирного тяготения. Пытливый ум, закалённый борьбой с непостижимым философским камнем, вскоре вывел из этого закона следствие, что Земля ведь должна быть у полюсов сплюснута сильнее, так как её экватор растягивается центробежной силой. Говоря научным языком, Земля является эллипсоидом вращения. Как диск.
Но центром научного мира была Академия Наук в Париже (знаменитая своим постановлением о том что «камни с неба падать не могут, ибо откуда им там взяться», которое на целый век запретило астрономам исследовать метеориты - впрочем, как видим, это заблуждение академиков имело под собой вполне рациональное обоснование). А Парижскую Обсерваторию в те годы возглавлял итальянский астроном и математик Джованни Доменико Кассини (жил в 1625 - 1712г), который совместно с сыном Жаком Кассини (жил в 1677 - 1756г) провёл измерения кривизны Земли в разных точках одного меридиана - и выходило по этим замерам, что Земля вытянута, но к полюсам. Как веретено.
Обрадованный учёный мир тут же с энтузиазмом занялся своим любимым делом - то есть бесплодными спорами. Враждовали французская и английская учёные школы, так что это противостояние можно считать последним отголоском Столетней Войны, разве что теперь вместо крови лились чернила. Наконец распри раскололи и саму Парижскую Академию. И только тогда академия занялась собственно наукой - в 1735г приняла решение послать сразу две экспедиции, чтоб замерить в точности длину дуги 1° широты у полюса и у экватора. Когда же точные замеры были получены, правота Ньютона была подтверждена. А Вольтер по этому поводу произнёс: «Он расплющил Землю и Кассини».
Из-за этой сплющенной формы Земли, как Ньютон и полагал, сила тяжести на экваторе меньше. Потому запуск космических ракет с экватора выгоднее, они действительно требуют меньше топлива. Даже спортивные достижения на экваторе лучше - у метателей и прыгунов в высоту. Но вот в горнолыжном спорте, где важна скорость скатывания вниз, как раз в северных странах рекорды устанавливают чаще. И, разумеется, сила тяжести влияет на дальнобойную артиллерию - так достоверно известно, что таблицы стрельбы для крупповской «Большой Берты» обстреливавшей Париж в Первую Мировую с дистанции в 135км, составлены не только с учётом кривизны Земли, но и с учётом силы тяжести в районе Парижа.
 | ||
 |
 Геодид (то есть модель) Земли с учётом гравитации выглядит вот так - но искривления модели специально преувеличены, глядя на нашу планету из космоса наш глаз не заметит отличий от шара
Геодид (то есть модель) Земли с учётом гравитации выглядит вот так - но искривления модели специально преувеличены, глядя на нашу планету из космоса наш глаз не заметит отличий от шара
|  |
 |
Для писателей-фантастов из этой истории есть поучительные выводы:
- закон тяготения неизбежно будет открыт (и военное дело, особенно развитие артиллерии, пусть даже не пороховой, этому способствует гораздо больше, чем яблочные сады) - а как только он открыт, форма планеты как идеального шара оказывается под справедливым сомнением
- как мы теперь знаем, Земля расплющена на какие-то 3 десятка километров, так что измерения парижским академикам пришлось провести точнейшие - и они справились с этой задачей. А ведь это ещё даже не Эпоха Паровых Машин. Это значит, что в Эпоху Пара цивилизация вступает с достаточно точными инструментами. И, добавим, довольно полными знаниями о планете на которой обитает
Паровой цивилизации, сложившейся в какой-нибудь уединённой долине или изолированном острове возникнуть не может! Либо эта «цивилизация» обломок более древней и глобальной, быть может её случайно уцелевшая от катаклизма (повального мора или иной катастрофы) колония. Версию о случайной находке древней библиотеки отбросьте сразу, так как даже если тексты написаны на понятном языке, то как постигнуть смысл научных понятий, которым у примитивного народа просто нет эквивалента? Вот попробуйте так с ходу взять современный учебник по конструированию, скажем, турбореактивных двигателей, и разобраться в нём - сразу поймёте каковы шансы даже величайшего мудреца среди пещерных людей воспользоваться секстантом по назначению.
Если есть желание выдумать логично непротиворечивый мир - то рецепт выше. Но...
Реальная история нашей планеты преподносит нам необъяснимые сюрпризы. Зачем древние вавилоняне хранили знания о необычайно точной градусной мере, никак не соответствовавшей их потребностям? Мы можем допустить, что они унаследовали эти знания (и передавали из поколения в поколение) от некой забытой цивилизации? Что ж, как гипотеза такое предположение допустимо. В конце концов, на обоих берегах Атлантического океана строили пирамидальные сооружения, что заставляет задуматься о существовавшей некогда связи культур - и по нашим представлениям о мореплавании того времени, без острова посреди океана такая связь невозможна. Но тут получается парадокс, даже вилка парадоксов:
- либо мы допускаем, что ОЧЕНЬ ДРЕВНИЕ массово плавали как минимум на «титаниках» с паровыми двигателями, ведь только так можно установить широкие культурные связи меж берегами океана - но этого конечно быть не могло
- либо допускаем существование в те времена мифической «Атлантиды» - которая разумеется была населена весьма технически развитой цивилизацией, имевшей насущную потребность в измерении всей планеты с точностью не хуже современной спутниковой системы навигации
Но я никак не могу понять как цивилизация с такими амбициями - а главное реальными познаниями о планете - вдруг ни с того ни с сего возникла на изолированном посреди океана острове...
Без хронометра не обойтись
То, что Земля шар, было известно очень давно, и прежде всего из наблюдений, в том числе астрономических. Астрономические же наблюдения показали, что Земля отнюдь не в центре мира, а обращается вокруг Солнца, к тому же имеет наклон оси. Видимое движение планет скверно укладывалось в систему геоцентрических небесных сфер, а уж законами физики эти сферы и вовсе объяснить было невозможно - тогда как модель Земли, вращающейся вокруг Солнца, отлично объясняла всё.
Зная это, можно вычислять положение светил на небосводе и составлять астрономические календари. А имея такие календари, можно удобно производить определение широты астрономическими методами.
Собственно широту определял, как мы знаем, ещё Эратосфен с помощью гномона. Действительно, достаточно дождаться самой короткой тени, что произойдёт ровно в астрономический полдень для данного места, и эта тень укажет нам и точное направление на север, и по отношению её длины к высоте гномона сможем вычислить угол падения солнечных лучей. Осталось только ввести поправку на положение Солнца относительно небесного экватора в этот день года, и широта определена.
Можно отправиться в Америку и там, даже с помощью примитивного гномона узнать свою широту. То есть параллель. То есть насколько мы смещены от экватора к полюсу. Но нужна ещё и долгота - то есть меридиан, или смещение к востоку или западу от избранной точки отсчёта.
И с XV века все великие морские державы (Испания, Голландия, Франция, Англия) объявляли денежные премии тому, кто предложит надёжный метод определения долготы.
Собственно ещё до нашей эры Гиппарх (о котором уже говорилось выше) предлагал одновременно наблюдать значительные астрономические явления, как, например, затмение. К примеру, на корабле наблюдают затмение в 4 часа пополудни, тогда как известно что в порте отплытия оно произошло ровно в полдень - следовательно корабль сместился к западу на 4 часа * 15° = 60°. Календарь затмений составляли ещё древне-египетские жрецы. Маленькая проблемка лишь в том, что солнечные и лунные затмения случаются в среднем 4 раза в год.
Но зароненная Гиппархом мысль искать решение на небе, нашла множество последователей, как только запахло деньгами. Так астроном Иоганнес Вернер (жил в 1468 - 1522г) предлагал измерять расстояние между звёздами и Луной. Но, увы, в то время ещё не существовало специальных инструментов для измерения положения между звёздами и Луной, неточно были определены положения звёзд, и даже сама траектория Луны на небе была не до конца изучена.
Галилео Галилей (жил в 1564 - 1642г) предлагал использовать наблюдения затмения лун Юпитера, которые сам же и наблюдал в свой телескоп. Этих затмений наблюдается тысяча в год, предсказать их было довольно просто, и методом пытались пользоваться - но вот наблюдения Юпитера вести возможно не всегда.
А кроме того, практически во всех случаях астрономического определения координат - по Солнцу ли, Луне, звёздам или затмениям - важно знать точное время, чтобы затем по астрономическим таблицам узнать из какого места Земли видно данное светило или явление под измеренным углом в данный час и минуту. Но как узнать этот час?
Простой инструмент гномон имел однако недостаток в том, что хорош для суши, но на качающейся палубе корабля совершенно бесполезен. Особенно если корабль идёт меняя галс - то есть угол к ветру - что парусникам приходилось делать нередко. Определить момент астрономического полудня по гномону на корабле не представляется возможным. К тому же, нас интересует не только местное время, но и время в порту отплытия - эта разница легко дала бы нам искомую долготу.
Пока лучшие астрономы бились над выбором удобного светила, проблему решил часовщик Джон Гаррисон (жил в 1693 - 1776г), сконструировавший точный морской хронометр. Во время плавания на Ямайку, по прибытии в Порт-Ройал два месяца спустя хронометр отстал всего на 5 секунд. Обратное плавание оказалось невероятно трудным, но за всё время путешествия общая ошибка составила только 1 минуту 54 секунды, что было даже меньше чем требования Комитета по долготе, учреждённого английским парламентом. Тем не менее, Комитет долгие годы отказывался выплатить часовщику причитающееся вознаграждение в размере 20 тысяч фунтов. Причина была банальна - парламентарии отказывались поверить в надёжность механизма даже после успешного испытания плаванием. Премию выплатить всё же пришлось, но это произошло много лет спустя.
Для фантастов из этой истории вывод таков: эпоха географических открытий и эпоха паровых машин идут практически рука об руку. Пока в дальние странствия отправляются отдельные смельчаки, можно обойтись вёслами и парусами. Но широкий транспортный поток нуждается в двигателе. А уж если есть двигатель, то конечно найдутся и желающие странствовать. Но где путешествия, там оказывается востребован механический пружинный хронометр. И обязательно появляется техническая возможность его изготовления. Век паровых машин без хронометров это нонсенс. Я бы добавил - без личных хронометров. Ведь хронометр Джона Гаррисона имел диаметр 13см, то есть уже укладывался в габариты настольных или каминных часов. Ещё немного миниатюризации и точный хронометр помещается в карман. А с началом воздухоплавания, пилоты аэропланов первыми начинают носить часы на руке, так как это при их профессии намного удобнее, чем носить их на цепочке (у воздухоплавателей таких проблем не было). А вот медсёстры, наоборот, носят часы в нагрудном кармане своего халата ещё долго-долго, в некоторых странах где сильна английская культура такой обычай можно встретить и поныне.
Откуда мерить долготу
 | ||
 |
 Тот самый маяк на острове Ферро от которого мерили долготу
Тот самый маяк на острове Ферро от которого мерили долготу
|  |
 |
С широтой определись просто. Экватор это 0° потому что в день равноденствия здесь Солнце в полдень прямо над головой. Полюс соответственно 90°, так как земная ось перпендикулярна плоскости экватора. Ну а любая параллель между ними может быть определена даже по методу Эратосфена. Сложнее с определением долготы. Тут одного лишь хронометра мало. С помощью хронометра можно получить разность в долготе между портом отправления и текущим меридианом корабля. Но как соотнести эту разность с картой?
Поначалу интересы государств в области картографии ограничивались максимум пределами своей страны. Соответственно можно было произвольно избрать точку отсчёта от которой вести промер земли и картографирование. Развитие морской торговли в мировом масштабе, а тем более появление заморских колоний, вызвали потребность в картографировании всей планеты. И вот тут уже пришлось договариваться о некой общей точке отсчёта. Какой меридиан считать нулевым?
Нынешний привычный нам Гринвический меридиан стал точкой отсчёта не так уж давно и лишь в угоду британской короне. А до него система была гораздо логичнее. Нулевым считался меридиан, проходящий через маяк на безлюдной скале острова Ферро (El Hierro) из Канарского архипелага - самой западной точки Старого Света. Таким образом, вся Европа оказывалась к востоку (с положительными координатами долготы), а вся Америка к западу (с отрицательными координатами долготы). Например на русских картах первой половины XIX века долготу как раз указывали от Ферро.
Но промерить в то время долготу до Ферро в точности не представлялось возможным. Потому приняли соломоново решение, что от Ферро до Парижа ровно 20° (впоследствии правда выяснилось что сам маяк находится от Парижа на 29' или 50км дальше, но решили ничего не менять). Ну а Париж был известен всему цивилизованному миру. Парижская академия наук центр научной мысли всей человеческой цивилизации того времени. Центр Парижской обсерватории отмечает точку Парижского меридиана, а он был избран в качестве эталона новой меры длины - метра, коих от полюса до экватора должно было уложиться на нём ровно 10 миллионов. Промерить сушу от Парижа было совсем не сложно и все государства рано или поздно это сделали. Включая и Россию, которая с тех пор писала на своих картах долготу от Парижа.
Самая точная карта
Идеальной карты не существует, что можно доказать и математически. Наиболее точная карта это глобус. К сожалению глобус достаточного для целей навигации масштаба будет слишком велик, вдобавок для работы с ним потребуются специальные инструменты. Поэтому штурманы используют карты на плоских листах бумаги, с которыми работают обычными циркулем и линейкой.
Не только идеальной карты не существует, но не существует даже идеальной проекции - то есть способа отображения Земли на плоскую карту. Любая проекция вносит те или иные искажения. Наконец, оказывается что для разных отраслей человеческой деятельности удобны разные проекции, разные правила представления планеты на плоскость. Где-то важна сетка меридианов и параллелей, где-то важно чтоб не искажалась площадь, а где-то можно пожертвовать и тем и другим, ради сохранения общей картины. Например, хорошо знакомая школьникам карта полушарий не сохраняет ни площадь материков, ни их форму, но зато хорошо позволяет показать ученикам картину Земли в общем.
Наверное наиболее удачна гномическая проекция Земли на правильный многогранник. Например, можно спроецировать нашу планету на куб, затем даже склеить его - получиться кубическая модель Земли.
 | ||
 |
+ увеличить картинку +
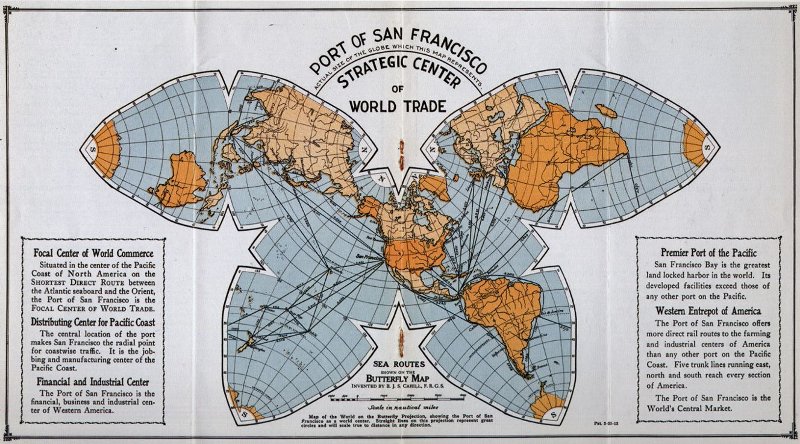 Карта Кэхилла в форме бабочки 1909 год
Карта Кэхилла в форме бабочки 1909 год
|  |
 |
Ещё эффектнее восьмигранная карта Кэхилла в форме бабочки 1909 года. А Ричард Бакминстер Фуллер в 1954г создал проекцию на икосаэдр, разместив Землю на его 20 треугольных гранях так, чтобы Северный полюс оказался примерно в центре, а континенты не разрезались (разрезы проходят по океанам). Правда он использовал не гномическую, а свою собственную проекцию под запатентованным названием Димаксион, которая отличается небольшими искажениями, причём распределёнными по карте достаточно равномерно.
 | ||
 |
+ увеличить картинку +
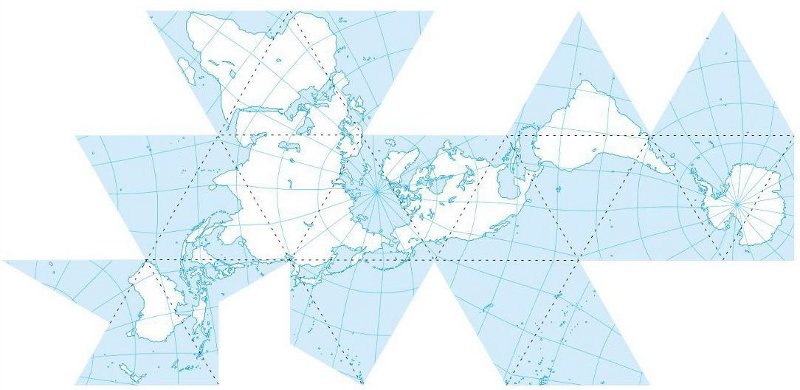 Карта Фуллера проекция Димаксион 1954 год
Карта Фуллера проекция Димаксион 1954 год
|  |
 |
Гномическая проекция одна из самых древних, но в Эпоху Возрождения использовалась редко (а в Средневековье про точность карт и вовсе никто не думал). Популярность приобрела в начале XVII века, особенно для карт звёздного неба. Важной для навигации особенностью этой проекции является то, что линия кратчайшего пути на картах в этой проекции - прямая, соединяющая выбранные точки. Кстати, на карте Кэхилла это хорошо заметно по проложенным на ней торговым морским маршрутам.
Завяжем узел
Метр удобен тем, что не зависит от размера ноги или руки какого-то человека (дюйм изначально произошёл от ширины большого пальца, но позже был установлен как 1/12 фута, а фут был в XII веке установлен как 1/3 ярда, который в свою очередь был взят как длина от кончика носа английского короля Генриха I до большого пальца его вытянутой руки). Тем не менее, упрямые моряки и поныне продолжают пользоваться морской милей.

Причина упрямства в удобстве. Это сухопутным крысам кажется, что морская миля неудобна - она не соотносится ни с верстой, ни с километром, ни даже с милей сухопутной. Зато она в точности равна 1 угловой минуте по окружности земного шара (конечно «в точности» только для тех времён). Если прокладывать путь корабля по глобусу, то длина пути по нему легко превращается в угловые минуты - а они в мили. Для штурмана очень удобно. При работе с плоской картой немного сложнее, но и тут есть правила построения дуг маршрутов и формулы вычисления из градусной меры.
Отсюда же происходит сохранившийся и поныне обычай измерять скорость корабля в узлах. Поначалу это действительно были узлы, завязанные через определённые промежутки на верёвке, привязанной к деревянному бруску. Всё вместе называлось лагом. Работало устройство так: матрос выбрасывал брусок за борт, и в течении минуты считал сколько узлов верёвки выскользнуло за борт. Расстояние же между узлами было подобрано так, чтоб в итоге скорость в узлах равнялась числу миль проходимых за час. Что, как мы уже понимаем, было опять же очень удобно для штурмана корабля.
На суше удобны меры длины, привязанные к физическим объектам, но море порождает иные способы измерения и свои собственные меры - которые неразрывно связаны с шарообразностью планеты и градусной мерой используемых карт.
май 2016г
Алексей «Рекс»

 Публикации
Публикации Программы
Программы Игры
Игры Товары
Товары рГоблин
рГоблин N. Значение этого простого метода поиска простых чисел было недооценено современниками Эратосфена, зато он активно используется и поныне - ведь простые числа входят во многие алгоритмы шифрования.
N. Значение этого простого метода поиска простых чисел было недооценено современниками Эратосфена, зато он активно используется и поныне - ведь простые числа входят во многие алгоритмы шифрования.