Секрет влекущей красоты
в которой читатель узнаёт отчего так милы нашем взору вещи Эпохи Пара
 | ||
 |  | |
 |
Секрет существует. И он реален. Никакой мистики, чудо совершил точный математический расчёт. И если вы хотите понять, а тем паче если хотите воссоздать вещь Эпохи Пара - то нужно познать и тайну этого секрета.
Художник или геометр
Малообразованный средневековый мастер творил наугад - но механик паровых машин действует наверняка, опираясь на математический расчёт. При этом он же не только механик, но ещё и дизайнер в современном понимании. Красота формы даже самой незначительной части машины для него важна, потому что иначе товар не продать. Да и, в отличие от современности, человек того времени воспитан в идеалах вечной красоты, а не быстро сменяющейся сиюминутной моды. А эталон красоты это золотое сечение, открытое ещё в Античности, и невзирая на все перемены моды, так и не покинувшее своего пьедестала. Не верите?
Золотому сечению подчинены пропорции фронтона Парфенона (одного из 7 античных чудес света) и портрета Джоконды (более известный как «Мона Лиза») кисти Леонардо Да Винчи (чуда Эпохи Возрождения). Наконец, этой же пропорции подчинены размеры кредитных карт (чуда современной банковской системы... м-да, до чего чудеса измельчали...)
Если предложить разным людям выбрать из нескольких с виду схожих прямоугольников самый приятный на вид, то люди выбирают прямоугольник, чьи стороны соотносятся по правилу золотого сечения. Даже если взять одинаково привычные нашему взгляду прямоугольники, соответствующие экрану телевизора, формату фотокарточки, листу бумаги для принтера - и среди них поместить золотой прямоугольник, то и тогда люди будут выбирать его.
Формула золотого сечения:
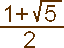 | = 1.6180339887... |
|---|
- 1 / φ = φ - 1
- φ² = φ + 1
- любая степень числа φ равна сумме двух предыдущих его степеней
Скажу Вам по секрету, число φ имеет непосредственное отношение к игре на финансовой бирже. Или к парламентским выборам, так как предсказание их результата то же подчиняется волновой теории Эллиота. Если биржевая котировка (или популярность политической партии) на взлёте, то, согласно этой теории, её следует умножать на число φ для получения ориентировочного прогнозируемого результата следующих торгов (или выборов). Ну а если котировка (партия) переживает падение, то умножив на величину обратную φ получим верхний предел новой стоимости (количества голосов избирателей). Впрочем, в эпоху паро-панка столь изощрённых предсказательных теорий ещё не могло существовать.
Но это была чистая арифметика, а нам для задач конструирования и дизайна интереснее геометрия. Геометрический смысл золотого сечения первым задокументировал Евклид примерно за 300 лет до нашей эры. Это такое деление отрезка при котором отношение всего целого отрезка к большей части было бы таким же, как отношение большей части к меньшей.
Вновь это соотношение открыто в Эпоху Возрождения Лукой Пачоли (1445-1517) в книге «О божественной пропорции» (De Divina Proportione) написанной в 1498г (опубликована в Венеции в 1509г, к тому времени автор успел подготовить уже три рукописи), а иллюстрации 60 многогранников к ней сделал сам Леонардо Да Винчи. В окончательном варианте добавились несколько глав, и среди них «Об архитектуре» (De Architectura), навеянная работами древне-римского архитектора Витрувия.
Собственно Возрождение это время, когда невежественные европейцы, едва перенявшие у арабов (в результате Крестовых походов) обычай мыться (да, до того немытость возводилась в святую добродетель! и немало было в средневековой Европе различных святых мужей, да что там мужей - даже принцесс, причисленных к лику святых, за то что годами не оскверняли себя мытьём... и потомки этих дикарей учат нас культуре?) - так вот эти невежественные люди вдруг открыли, что живут на руинах древней величественной цивилизации, что ходят ногами по триумфальным колоннам и прекрасным статуям Античности, что за полтора тысячелетия до них были водопровод, бани, канализация, довольно совершенные механические насосы и даже автоматические мельницы... список неожиданных открытий можно продолжать.
Марк Витрувий Поллион был архитектором при Юлии Цезаре, в I веке до н.э. Работы его были переведены в Эпоху Возрождения в 1486г и сразу же завоевали популярность. Витрувий вывел канон красоты из простых наблюдений. Средне-статистический человек имеет рост равный размаху рук, а если лежащий на спине мужчина разведёт в стороны ноги и руки, то его фигура будет вписана в окружность. Первому, следуя этим указаниям Витрувия, совместить две фигуры, одна из которых вписана в квадрат, а другая в круг, удалось Леонардо Да Винчи. Его решение «Витрувианского человека» заключалось в том, что центры фигур различны: для круга центром является пупок, а для квадрата гениталии.
(есть мнение, что сама идея именно такого совмещения центров принадлежит одному из друзей Леонардо, но именно Да Винчи сумел воплотить идею в рисунок)
 | ||
 |
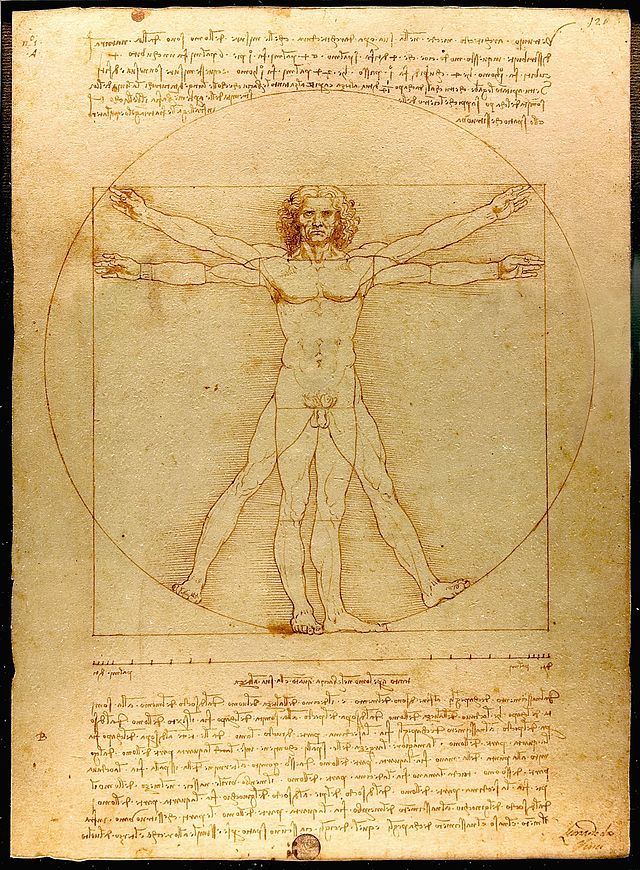 «Витрувианский человек» Леонардо Да Винчи
«Витрувианский человек» Леонардо Да Винчи
|  |
 |
Золотое сечение можно назвать непреложным каноном дизайна изящных времён. В ещё одном трактате Луки Пачоли «Сумма арифметики, геометрии, дробей, пропорций и пропорциональности» (Summa de Aritmetica, Geometria, Proportioni et Proportionalita) (опубликован в Венеции в 1449г, содержит более 600 страниц) прямо написано: «Религиозные службы имеют небольшую ценность, если церковь не была построена в правильной пропорции». Для человека того времени поставить божественное ниже созидаемого человеком это либо кощунство - либо высшая истина.
Наконец упомянем Альбрехта Дюрера, известного нам своими гравюрами, а современникам ещё и как видный военный инженер, внёсший свой вклад в рациональное конструирование крепостей. Разумеется этот видный математик был последователем идей Да Винчи (да иначе и быть не могло, Леонардо стал кумиром и идеалом на многие века). На гравюрах к своей книге «Об измерениях» (полное название «Руководство к измерению циркулем и линейкой»), Дюрер изобразил свой метод построения модели в перспективе, что было новшеством для того времени. Там же разобрано построение сечений конуса (например, получение параболы). А ещё описываются различные геометрические тела и среди них спираль на основе золотого сечения, в то время даже получившая имя спирали Дюрера.
 | ||
 |
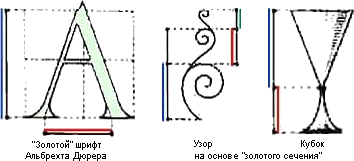
|  |
 |
Философия Дюрера о красоте высказана им одной фразой:
«Красота заключается в гармонии частей друг с другом - и с целым»
Нетрудно догадаться какое именно соотношение он считал гармоничным.
Именно стиль работ Дюрера и надо брать за отправную точку энтузиастам паро-панка.
Поиграем с идеалом
Что интересного с практической точки зрения даёт эта золотая пропорция?
Возьмём пару одинаковых золотых прямоугольников. Проведём на одном из них диагональ. Второй же приложим к торцу первого, так чтоб получилась буква «Г» (или «L») - и чудо, диагональ продолжается по прямой до следующего угла! Если описать новый большой прямоугольник по этим двум, то он окажется золотым.
Ещё интереснее поиграть в деление большого золотого прямоугольника. Отрежем от него квадрат - и получим в оставшейся части новый золотой прямоугольник. Мало того, если провести диагональ большого прямоугольника и диагональ малого - то окажется что они пересекаются всегда под прямым углом.
Но самое забавное, что если продолжать процесс деления - резать квадратами всё новые получающиеся малые золотые прямоугольники - то окажется что даже диагонали самого большого и самого малого из полученных золотых прямоугольников пересекаются точно под прямым углом.
 | ||
 |
Конечно, природа не ограничена одной лишь золотой пропорцией. Существуют и другие замечательные прямоугольники - например, с соотношением сторон |  |
 |
От деления золотого прямоугольника квадратом всего один шаг до логарифмической спирали. Возьмём всё тот же многократно делённый большой золотой прямоугольник, но теперь будем вписывать в каждый имеющийся в нём квадрат дугу с радиусом равным диагонали этого квадрата. И, взгляните, дуги стыкуются одна за другой в спираль, которая называется логарифмической.
 | |||||||
 |
|  | |||||
 |
Строго говоря, этим методом мы построили не точную логарифмическую спираль, а приближённую. Но обычно и такого приближения вполне достаточно.
Спираль эта интересна двумя свойствами:
- она подобна самой себе - то есть хотя расстояние между витками очевидно увеличивается с каждым витком, но вот соотношение между ними остаётся неизменным
- угол от линии спирали к центру в любой её точке постоянен
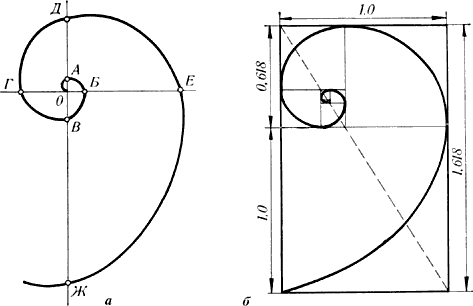
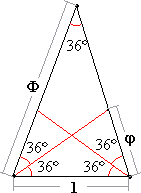
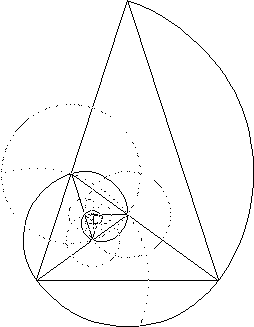
Построить более точную логарифмическую спираль поможет золотой треугольник. Это равнобедренный треугольник с углом при вершине 36° и по 72° у основания, соотношение его большей стороны к меньшей как раз в точности равно золотой пропорции. Десяток таких треугольников ровно укладываются в круг, позволяя построить из своих коротких сторон правильный десятиугольник.
 | ||||
 |
|  | ||
 |
Но нам интереснее спираль. Для этого разделим наш большой золотой треугольник перпендикуляром от любой длинной стороны к противолежащей вершине (это будет вершина при основании) - получим два треугольника, меньший из которых снова золотой. Продолжим процесс многократно, как делали это с прямоугольником. А теперь начиная с самого меньшего треугольника, из его вершины (что против основания) проводим дугу, радиусом равным длине длинной стороны. И так повторяем с каждым треугольником по возрастающей - и получаем логарифмическую спираль.
 | ||
 |
И опять же заметим, что мир не ограничен одной лишь логарифмической спиралью, сколь бы красивой и гипнотически заманчивой она ни была. В технике куда чаще приходится иметь дело со спиралью Архимеда. Если, к примеру, наматывать верёвку (на плоскости) вокруг стержня, то увидим такую спираль. 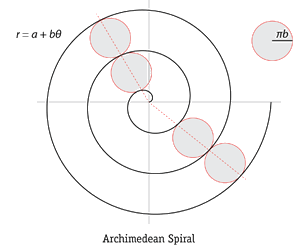 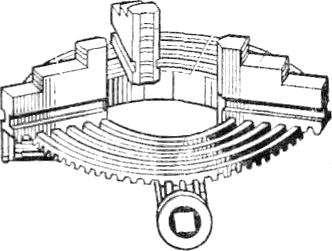 |  |
 |
Не перегибай!
Во времена развитого социализма бытовала шутка с политическим подтекстом: «Если слишком круто взять влево, то можно провернуться и сделаться правым». Если слишком увлечься идеальной красотой, то можно сделаться Малевичем и закончить своё творчество идеальным «Чёрным квадратом». Конечно, как гласит народная мудрость «на вкус и цвет товарища нет», но мы ведём речь о времени, когда люди не считали квадрат изящной фигурой достойной высшего восхищения, а предпочитали более замысловатые формы.
А теперь посмотрите то, что окружает нас нынче. Вот iPad - не правда ли, совершенство? Ведь в нём золотая пропорция! Но взгляните на коробку сигарет... да, она то же в золотой пропорции (неужто из-за этой идеальной формы пачки сигарет, пагубная привычка кажется такой привлекательной для молодёжи?). А вот взгляните на здание ООН в Нью-Йорке - коробка коробкой (помните как Владимир Высоцкий пел в одной из своих юмористических песенок «На горе стояло здание ужасное, издаля напоминавшее ООН»). Однако ж по пропорциям эта коробка безупречна, ведь в ней аж 3 золотых прямоугольника. Стало быть идеал красоты.
Всё это - iPad, пачка сигарет и здание ООН, как впрочем и многое другое что окружает нас - просто прямоугольные коробки! Неужели идеал человечества - жить среди прямоугольников? Пусть даже и золотых...
Виновник этого цивилизационного заблуждения - Ле Корбюзье (настоящее имя Шарль Эдуар Жаннере-Гри, 1887-1965), уроженец Швейцарии, но позже получил французское гражданство и именно будучи французом приобрёл мировую известность как величайший архитектор современности. Даже Трамп, нынешний президент США и вне сомнения хороший архитектор - и то никогда не будет столь же прославлен. Ведь Ле Корбюзье был не просто хорош - он был гениальный творец, каких боле не будет. А ещё у него были и деньги и связи - в придачу к таланту, причём таланту многогранному. Он оставил след абсолютно во всех областях дизайна (в частности именно он изобрёл шезлонг). Но главное направление это конечно же архитектура, в коей он ещё при жизни был признан гением. Неудивительно, что он участвовал в международной комиссии по проектированию здания ООН, а завершал проект его ученик Нимейер.
Быть может он оказался ослеплён своим успехом, а может не давали покоя лавры Ветрувия, только он решил создать нечто очень значительное для всего человечества, а именно - подарить миру свою систему мер. Зачем? Отчего-то он выдумал сам для себя, что метрическая система мер противна человеческой природе. Якобы связь с пропорциями человеческого тела утрачена и оттого строить удобные для людей дома стало невозможно. А вот в былые славные времена дюймов, футов и ярдов...
Прав ли был великий архитектор в своём предположении?
Немало исследователей старины находят в древних мерах длины некое совершенство. А порой без сомнений указывают на их связь с золотой пропорцией. Но так ли это? К примеру, «серьёзные научные работы», доказывая красоту храмов Древней Руси, связывают сию красоту с особенностями старо-русских мер длины - а они де непременно основаны на золотой пропорции. Тут возражений нет, как мы видели выше, люди интуитивно могут выбирать объекты, соответствующие золотой пропорции. И нет причин, почему бы такой объект не мог быть принят в качестве эталона мер. Но где же та самая древняя мера?
Увы, современные археологи пока не раскопали тот самый эталон древних. А где же тогда взять подтверждение гипотезы? И вот для доказательства своей правоты иные авторы выбирают, к примеру, сажени совершенно произвольно - из разных губерний, разных областей применения, даже разных веков. Затем пытаются их соотнести. Не получается? Тогда начинается игра в числа. Вплоть до того, что в формуле золотой пропорции меняют знак! Если же и это не помогает, то находят другое соотношение - например, не так уж редко можно встретить соотношение 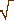 2 - как мы знаем, только оно даёт экономный раскрой прямоугольных листов материала. К примеру полотна. Почти наверняка нашим далёким предкам приходилось кроить холсты и разумеется они хотели добиться самого экономного раскроя. Так что неудивительно, если методом проб и ошибок они нашли замечательное соотношение. Но современные авторы не утруждают себя математикой, о замечательных прямоугольниках не слышали, а просто объявляют что вот же она, искомая золотая пропорция!
2 - как мы знаем, только оно даёт экономный раскрой прямоугольных листов материала. К примеру полотна. Почти наверняка нашим далёким предкам приходилось кроить холсты и разумеется они хотели добиться самого экономного раскроя. Так что неудивительно, если методом проб и ошибок они нашли замечательное соотношение. Но современные авторы не утруждают себя математикой, о замечательных прямоугольниках не слышали, а просто объявляют что вот же она, искомая золотая пропорция!
На деле золотая пропорция только одна и это
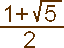 | = 1.6180339887... |
|---|
Древние меры длины были связаны с человеком не из неких мистических, а из самых практических соображений - эти меры всегда под рукой. Русский плотник брал верёвку и на ней вязал узлы по размаху своих рук (маховая сажень, она же обычно равна росту человека) или по росту с вытянутой рукой (косая сажень). Аналогично поступал и англичанин, примеряя дюйм к пальцу, а фут к ступне. А за тысячи лет до них, древний египтянин отмерял расстояния, прикладывая собственную руку, от кончика пальцев до локтя. Но пальцы, руки и ноги бывают разными. Возникла проблема стандартизации и её пытались решить. К примеру, в одном городе брали дюжину людей первыми вышедших из церкви в воскресенье, и их средняя длина стопы объявлялась эталоном. Наконец, ярд был определён как расстояние от вытянутой руки до кончика носа английского короля, измерен и установлен эталоном. С этого момента ярд делился ровно на 3 фута, вне зависимости от реальных стоп, а дюйм получался делением фута на 12 частей, невзирая на размеры реальных пальцев.
Только стандартизация мер длины, их отрыв от размера тела конкретного человека, позволяют скоординировать труд коллектива людей, возводящих великолепное здание. И, разумеется, этому множеству строителей удобнее считать футы или сажени целыми числами, а не дробным числом, пусть даже и золотого соотношения.
Но Ле Корбюзье влюбился в золотую пропорцию. Ведь именно в этом секрет красоты древних построек. И, следуя далее по пути таких размышлений, великий архитектор XX века, по аналогии с древним «Витрувианским человеком», выдумал своего «Модулора». Причём ужасно гордился этим:
«Метр, сантиметр, дециметр - эти единицы не отражают человеческие пропорции, а Модулор отражает»
Есть и статуя Модулора, изготовленная по тем самым выведенным Ле Корбюзье идеальным пропорциям. Одного взгляда достаточно, чтобы как говорится без комментариев...
 | ||
 |
 Статуя Модулора
Статуя Модулора
|  |
 |
К несчастью для человечества случилась Вторая Мировая война. К несчастью ещё и потому, что изящная архитектура в эти годы не востребована, Ле Корбюзье оказался не у дел, и потому с маниакальным упоением погружается в свои изыски. Между 1942 и 1948 годами он разрабатывает Модулора как систему мер для строительства и дизайна на основе золотого сечения и пропорций саксонского антропологического типа. К этому типу принадлежат типичные жители Северной Европы. Рост типичного мужчины 182см. А подняв вверх руку он достал бы до потолка на высоте в 226см. И, наконец, пупок находится точно на высоте 113см - то есть делит высоту до потолка ровно пополам, притом больше расстояния от пупка до макушки в столько же раз, во сколько то больше оставшегося расстояния до потолка - и разумеется это соотношение равно φ. Так что с точки зрения следования золотой пропорции всё должно было быть идеально.
 | ||
 |
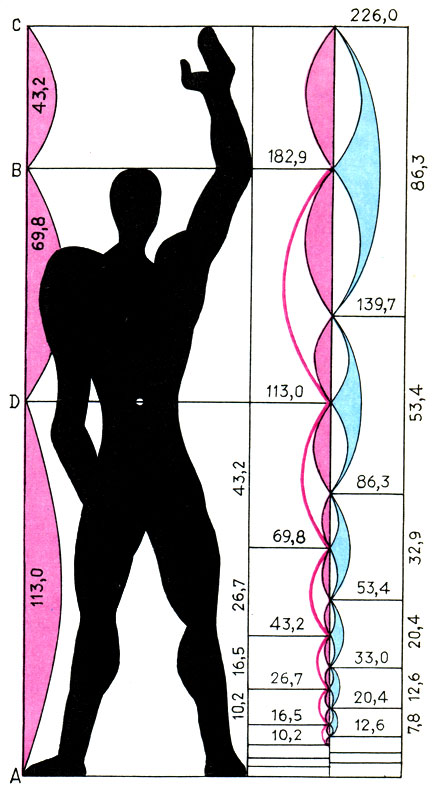 Система пропорций Ле Корбюзье «Модулор»
Система пропорций Ле Корбюзье «Модулор»
|  |
 |
Книга «Модулор» издана в 1950г с огромным успехом. А уже в 1955г появляется «Модулор 2». Но зачем? Да затем, что оказалось нужно строить и в Южной Европе, а там типичный рост мужчины латинского типа 172см. Не вышло универсальной системы мер!
Возмутительный (для феминисток) факт: про женское тело вспомнили только под конец создания «Модулора 2». И... отбросили. В общем понятно почему - представьте себе Модулора-даму :-0
Впрочем, феминистки могут утешится тем, что они не одиноки в своём несчастье. Точно так же Модулор игнорирует детей, подростков, а заодно добрую треть взрослых, но низкорослых жителей этой планеты (таких как большинство населения Юго-Восточной Азии).
 | ||
 |
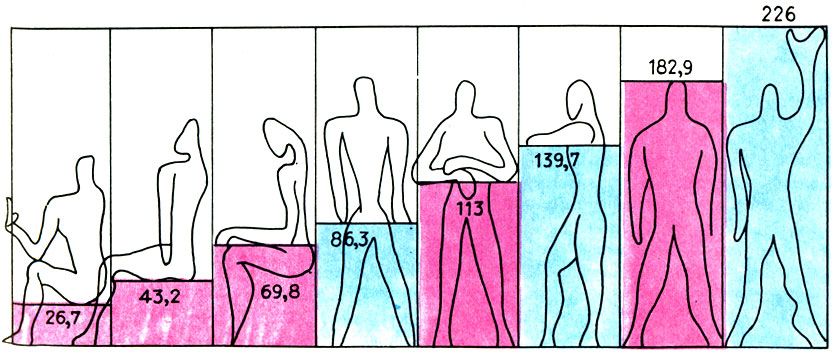 По замыслу Ле Корбюзье все вещи следовало делать удобными для Модулора
По замыслу Ле Корбюзье все вещи следовало делать удобными для Модулора
|  |
 |
Факт: по собственному признанию Ле Корбюзье в школе с отвращением решал математические задачи и лишь с годами признал, что от математики бывает польза. Его математическое невежество вполне показывает одна из первых попыток создать Модулора, когда (уже будучи владельцем архитектурной фирмы) он дал своему помощнику задание описать вокруг человеческой фигуры прямоугольник из двух поставленных друг на друга квадратов, а затем разместить третий квадрат опираясь на вписанный в прямоугольник прямой угол. Представьте, для него явилось открытием, что вписанный прямой угол разделил прямоугольник из двух квадратов точно посередине!
По-видимому, из-за слабого знания математики, Ле Корбюзье даже не подозревал о золотом треугольнике - но буквально бредил прямоугольниками. Он мечтал построить целый прямоугольный город. Главное чтоб соотношение сторон - что у здания, что у целого города - было как у золотого прямоугольника. Чем будет такой город удобен для жителей неясно. Зато очевидно, что строительные трудности при такой планировке сильно увеличиваются, ибо Земля почти нигде не даёт человеку ровного прямоугольного поля чтоб хватило даже на маленький городок. Придётся приспосабливаться к холмам, оврагам, рекам - что нарушит правильную прямоугольность города. Либо засыпать и сровнять их, в очередной раз победив природу... но добавит ли нам это счастья? Уже не раз побеждали - а счастья от этого так и не видели.
Была бы польза для строителя от системы мер Модулора? Вот кирпич. Он имеет пропорции длины к ширине как 1:2, что нужно для надёжного перекрытия рядов при кладке стены - это совсем не соответствует золотой пропорции. Из века в век его вес и размер определяется ухватистостью одной рукой каменщика. А толщина стен и поныне берётся в кирпич, два или три - что никак не соотносится со шкалой Модулора.
Похоже великий архитектор мыслил и творил в каком-то собственном отвлечённом мирке, а нужды реальных людей его не волновали. Показательна его Марсельская жилая единица (Unite d’Habitation) - многоквартирное здание, все внутренние пространства которой основаны на пропорциях системы Модулора. Квартиру этой Марсельской жилой единицы могут видеть поклонники сериала «Звёздный крейсер Галактика» в некоторых сценах счастливой жизни на планете (другие здания в этом сериале так же отчётливо напоминают различные творения Ле Корбюзье). Очевидно, что быть может такое жильё ещё подойдёт одинокому молодому горожанину из тёплого Марселя, который разве что изредка приводит к себе домой подругу на ночь. Но уже для семейного марсельца это жильё неудобно. А уж для сибирского крестьянина...
 | ||
 |
 Марсельская жилая единица
Марсельская жилая единица
|  |
 |
Марсельская жилая единица спроектирована и построена в 1946—1950г. Это первый масштабный эксперимент Ле Корбюзье по введению в конструирование Модулора. Шаг колонн 419 см составлен из двух размеров по синему ряду — расстояния в чистоте 366 см и толщины конструкции 53 см. Высота помещений 226 см и толщина перекрытия 33 см (высота этажа 259 см) также соответствуют синему ряду. Из этих размеров следует, что основная сетка фасада как в чистоте между конструкциями 366 х 226 см, так и в осях 419 х 259 отвечает пропорции золотого сечения. Основная сетка получает дополнительные членения по вертикали, казалось бы, сложный ритм которых достигается лишь тремя размерами по красному ряду; один из этих размеров, равный половине высоты этажа 113 см, членится в золотом сечении на 70 и 43 см.
Может быть внешне это для кого-то и выглядит красиво (ой, столько золотых прямоугольничков!), но даже в «хрущобах» до потолка 250см - и то мы жалуемся что низковат. То есть потолок идеального жилого пространства вообще нависает у жильца над головой, создавая гнетущее напряжение и уж точно не способствуя свободному току воздуха, так важному для вентиляции помещения (а ведь в жилых зданиях этому должно уделяться особое внимание, иначе жильцам обеспечены хронические болезни дыхательных путей). Обнаружив эту строительную ошибку, хитрый сын швейцарско-подданного был вынужден сделать квартиры двухэтажными. Но в итоге получил избыточное пустое пространство и избыточную вентиляцию, что делает неприменимым его творение для местностей холоднее тёплого Средиземноморья.
Нет, не существует, невозможно создать унифицированную для всех систему жилья. Как не получился универсальный Модулор, так и универсальное жильё на его основе не удалось.
Ошибка Ле Корбюзье как архитектора заключалась в том, что вместо того чтобы осмыслить функциональность жилья (ведь очевидно, что функциональность хлева и спальни различна) и из этого создавать действительно удобную форму, он поступил не просто «прямо наоборот», а даже ухитрился сделать ещё хуже - взяв за основу некую абстрактно исчисленную цифру, на ней одной построил форму, и возвёл её в абсолют. Быть может цифру он вычислил и верно. Да вот только подход «от обратного» и результат в итоге дал обратный.
Ведь Ле Корбюзье видел вместо реальных людей только своего аморфного и абстрактного Модулора. И жильё и всё прочее творил для этого бездушного истукана. Лучшее подтверждение этому, его собственный рисунок, где всякая вещь идеально соответствует Модулору (и его числовому ряду, созданному на основе золотой пропорции) - но вряд ли найдётся на всей планете хоть один живой человек, которому все эти вещи оказались бы столь же удобны.
 | ||
 |
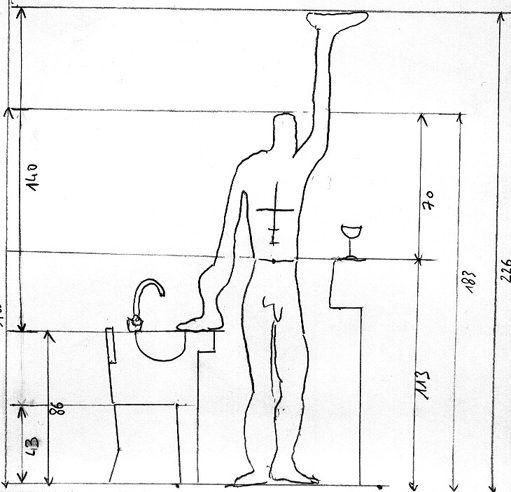 Рисунок самого Ле Корбюзье, иллюстрирующий концепцию применения Модулора в планировке помещений
Рисунок самого Ле Корбюзье, иллюстрирующий концепцию применения Модулора в планировке помещений
|  |
 |
Однако такой подход оказался весьма технологичным и востребованным большой промышленностью. И потому теперь мы носим штампованную одежду, ездим в штампованных авто, живём в домах, одинаковых настолько, что новостройки из разных городов легко перепутать, как в советской комедии «С лёгким паром». Скажите за это спасибо Ле Корбюзье, ведь именно он применил всё своё влияние, чтобы создать именно такое счастливое будущее для нас всех. Унифицированное будущее (универсальные магазины, мода уни-секс...а теперь уже в развитых демократических странах вместо «мужа» и «жены» следует говорить «родитель 1» и «родитель 2» - что подвергнется унификации дальше?).
Справедливым будет сказать, что Ле Корбюзье (при всём уважении к его дизайнерским талантам) в делах требующих строгого и взвешенного расчёта (как математика, геометрия, конструирование и даже система мер) проявил себя как типичный дилетант - то есть, не разобравшись ещё в вопросе, уже принялся всё переиначивать. И если некоторые изобретения (как шезлонг) ему случайно удались, то остальное уж лучше б он не трогал вовсе. Но на беду для человечества этот дилетант оказался при деньгах, со связями и уже состоявшимся именем основателя великой архитектурной школы, которому никто не осмеливался перечить. А хуже всего то что его неразумные предложения оказались выгодны всепожирающему конвейеру промышленности, штамповавшему унифицированный ширпотреб и просто-таки мечтавшему о унифицированном потребителе. По злой иронии судьбы именно то, против чего Ле Корбюзье искренне собирался бороться - против бездушия в дизайне вещей для людей - он же сам своим неумеренным энтузиазмом и возвёл на пьедестал, подменив живого Человека - бездушным Модулором.
Однако в Эпоху Пара это ещё не произошло. Если угодно, паро-панк даёт Вам необычную возможность провернуть колесо времени назад, когда призрак унифицированного модулора ещё не нависает над планетой. И потому в том старом-добром-наивном мире каждую вещь делают тщательно и подгоняют под заказчика. Так что даже продукция с конвейера мануфактуры будет в итоге обладать индивидуальными чертами владельца.
Вместо напутствия
Дизайнер в стиле паро-панк должен... нет, просто ОБЯЗАН проникнуться мышлением тех времён, когда существовал сплав науки и искусства в единое целое. Именно сплав - в коем наука и искусство неразрывно идут рука об руку. И этот сплав и красив и рационален, и прекрасен и удобен одновременно. И так абсолютно во всех отраслях, во всех сферах жизни и у всех слоёв общества. По правде сказать в современном мире редкая элитарная вещь может сравниться по практичности с ширпотребом тех времён.
Вам нужно здорово переиначить своё мышление, чтобы создать что-то по-настоящему паро-панковское.
И помните, что по мнению современников никто не превзошёл Леонардо да Винчи в искусстве рисования, но сам он начинает свой «Трактат о живописи» (Trattato Della Pittura, написан около 1498г, но опубликован лишь полвека спустя) словами:
«Пусть никто, не будучи математиком, не дерзнёт читать мои труды»
Вы привыкли думать о себе, как о гуманитарии. Вам неинтересны точные науки, ведь ваше поприще совсем иное...
Выбросьте эту чушь из головы! Немного математики ещё никому не повредило. Сам непревзойдённый Леонардо не гнушался математикой. И потомкам велел познать математику прежде рисования. Следуйте этому завету великого мастера. Он знал, о чём говорил.
май 2016г
Алексей «Рекс»

 Публикации
Публикации Программы
Программы Игры
Игры Товары
Товары рГоблин
рГоблин